小学数学总复习专题讲解及训练(七)

　　主要内容

　　正比例和反比例

　　学习目标

　　1、使学生结合实际情境认识成正比例和反比例的量，能根据正、反比例的意义判断两种相关联的量是否成正比例或反比例。

　　2、使学生初步认识正比例的图像是一条直线，能利用给出的具有正比例关系的数据在方格纸上画出相应的直线，能根据具有正比例关系的一个量的数值看图估计另一个量的数值。

　　3、使学生在认识成正比例、反比例的量的过程中，初步体会数量之间相依互变的关系，感受有效表示数量关系及其变化规律的不同数学模型，进一步提升思维水平。

　　4、使学生进一步体会数学与日常生活的密切联系，增强探索数学知识和规律的意识，养成积极主动地参与学习活动的习惯，提高学好数学的信心。

　　考点分析

　　1、两种相关联的量，一种量变化，另一种量也随着变化。如果这两种量中相对应的两个数的比的比值(也就是商)一定，这两种量就叫做成正比例的量，它们之间的关系叫做正比例关系。

　　如果用字母x和y分别表示两种相关联的量，用k表示它们的比值，正比例关系可以用这样的式子来表示：= K(一定)。

　　2、用“描点法”可以得到正比例的图像，正比例的图像是一条直线。对照图像，能根据一种量的值，估计另一种量相对应的值。

　　3、两种相关联的量，一种量变化，另一种量也随着变化。如果这两种量中相对应的两个数的乘积一定，这两种量就叫做成反比例的量，它们之间的关系叫做反比例关系。

　　如果用字母x和y分别表示两种相关联的量，用k表示它们的积，反比例关系可以用这样的式子来表示：xy = K(一定)。

　　4、两个变量的比值一定，这两个变量成正比例;两个变量的积一定，这两个变量成反比例;没有上述两种关系，这两个变量不成比例。

　　典型例题

　　例1、(正比例的意义)一列火车行驶的时间和路程如下表。这两种量有什么关系?

　　分析与解：

　　(1)从上表可以看出，表中有时间和路程两种量。

　　(2)从左往右看，时间扩大，路程也扩大;从右往左看，时间缩小，路程也缩小。所以它们是两种相关联的量。

　　(3)路程和时间的比值始终不变，……这个比值就是火车的行驶速度。

　　通过观察和计算，我们对路程和时间的关系有两点发现：第一点路程和时间是两种相关联的量，也就是时间变化，路程也随着变化;第二点路程和对应的时间的比的比值(也就是速度)是一定的，有这样的关系：

　　具备了这两个条件，我们就可以得到结论：行驶的路程和时间成正比例关系;行驶的路程和时间成正比例的量。

　　点评：判断两种量是不是成正比例，分三步：一看它们是不是相关联的两种量;二是看一种量变化，另一种量是不是也随着变化;满足了前面两个条件，再看它们的比值是否一定。不要省去任何一步。如果用字母x和y分别表示两种相关联的量，用k表示它们的比值，正比例关系可以用这样的式子来表示：

　　例2、(判断是否成正比例)

　　练习本的单价一定，买练习本的数量和总价是不是成正比例?为什么?

　　分析与解：根据正比例的意义，看两个变量的比值是否一定，如果两个变量的比值一定，那么这两个变量就成正比例，反之，则不成正比例。

　　买练习本的数量和总价是两种相关联的量，它们与练习本的单价有下面的关系：

　　所以练习本的数量和总价成正比例。

　　例3、(正比例的图像)磁悬浮列车匀速行驶时，路程与时间的关系如下。

　　(1)图中的点A表示时间为1分钟时，磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。

　　(2)连接各点，它们在一条直线上吗?

　　(3)根据图像判断，列车运行2分半钟时，行驶的路程是多少千米?行驶30千米大约需要几分钟?

　　分析与解：根据提供的各组数据描出图像的许多个点，再依次连成直线。路程和时间相对应的数的比值都是7，即速度一定，路程和时间成正比例，图像是一条直线。对照图像，可以根据时间的值估计出路程的值，也可以根据路程的值估计出时间的值，估计时允许有一定的出入。

　　(1)描点、连线如图。

　　(2)在一条直线上，因为路程和时间成正比例，正比例的图像是一条直线。

　　(3)根据图像，列车运行2分半钟时，行驶的路程是17.5千米;行驶30千米大约需要4.3分钟。

　　例4、(辨析)圆的周长和直径成正比例，圆的面积和半径成正比例?

　　分析与解：圆的周长和直径成正比例，而圆的面积和半径却不成正比例。

　　可列表判断。

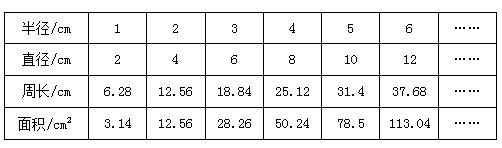
　　圆的周长和直径的相对应的数的比值都是3.14，所以圆的周长和直径成正比例。而圆的面积和半径的相对应的数的比值是变化的，所以圆的面积和半径不成正比例。

　　圆的周长和直径成正比例，圆的面积和半径却不成正比例。

　　例5、(反比例的意义)

　　下表是王师傅加工一批零件时，每小时加工零件个数随时间变化的情况。这两种量有什么关系?

　　分析与解：

　　(1)从上表可以看出，表中有每小时加工零件的个数和加工的时间两种量。

　　(2)从左往右看，每小时加工零件的个数扩大，加工的时间反而缩小;从右往左看，每小时加工零件的个数缩小，加工的时间反而扩大。所以它们是两种相关联的量。

　　(3)每小时加工零件的个数和相对应的加工的时间的积都始终不变，如20 × 12 = 240，30 × 8 = 240，40 × 6 = 240……而这个积就是这批零件的总个数。

　　通过观察和计算，我们发现：每小时加工零件的个数和加工的时间是两种相关联的量，每小时加工零件的个数随着加工的时间变化而变化，但无论它们怎么变化，相对应的积是一定的，有这样的关系：每小时加工零件的个数 × 加工的时间 = 零件的总个数(一定)。

　　所以每小时加工零件的个数和加工的时间成反比例的量，它们之间的关系叫做反比例关系。

　　点评：判断两种量是不是成反比例，和正比例一样，分三步：一看它们是不是相关联的两种量;二是看一种量变化，另一种量是不是也随着变化;满足了前面两个条件，再看它们的乘积是否一定，进行判断。不要省去任何一步。如果用字母x和y分别表示两种相关联的量，用k表示它们的比值，正比例关系可以用这样的式子来表示：xy = K(一定)。