例 7 有 8 个不同约数的自然数中，最小的一个是多少?

　　解：设有 8 个不同约数的自然数为 N，根据例 8 后的说明来分析 N 的取 值可能性。

　　因为 8=7+1=(1+1)·(3+1)=(3+1)·(1+1)=(1+l)·(1+1)·(1+l)，所以 N 只能为下面四种形式：

　　(1)N=a⁷ (3)N=a³×b

　　(2)N=a×b³ (4)N=a×b×C

　　(a、b、c 为不同的质数)

　　要使 N 最小，可以用 a=2，b=3，C=5 去代入上面四个等式，分别得到 N 为 128、54、24、30。所以有 8 个不同约数的自然数中最小的一个是 24。

　　答：最小的一个是 24。

　　例 8 (中国古代问题) 今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何?

　　这一问题可译为：一个数除以 3 余 2，除以 5 余 3，除以 7 余 2，求适合这些条件的最小数。

　　解法 1：用枚举法。

　　(1)除以 3 余 2 的数有：5、8、11、14、17⋯⋯;

　　(从第二个数起，每一个数都比它的前一个数多 3)

　　(2)除以 5 余 3 的数有：8、13、18、23、28、⋯⋯。

　　(从第二个数起，每一个数都比它的前一个数多 5)

　　显然 8 被 3 除余 2，且被 5 除余 3。因为 3 与 5 的最小公倍数是 15，所 以 15+8、15×2+8⋯⋯15×n+8，都同时满足被 3 除余 2，被 5 除余 3 这两 个条件，只须在这列数中找到被 7 除余 2 的最小数。为此只要用 n=1、2、3、4、⋯⋯依次去代入 15×n+8。当 n=1 时，15×1+8=23，23÷7=3⋯⋯2 所以 符合题意的数是 23。

　　解法 2：

　　(1)从 5 和 7 的公倍数 35、 70、 105⋯中找出除以 3 余 2 的最小数是 35。

　　(2)从 3 和 7 的公倍数 21、 42、63、⋯中找出除以 5 余 3 的最小数是 63。

　　(3)从 3 和 5 的公倍数 15、30、45、⋯中找出除以 7 余 2 的最小数是30。

　　所以 35+63+30=128 能符合“被 3 除余 2、被 5 除余 3、被 7 除余 2”。 又因为 3、5、7 的最小公倍数是 105，由此得符合题意的数是 128-105×1=23。

　　答：适合这些条件的最小数是 23。 说明：这个问题是驰名中外的中国古代问题之一。解答这类问题要用到古代数学家孙子所发明的著名定理——“孙子定理”，它的解法很早就流传到国外，被称为“中国剩余定理”。

　　例 9 一个数减去 1 能被 2 整除，减去 2 能被 5 整除，减去 3 能被 7 整 除，加上 4 能被 9 整除，这个数最小是多少?

　　(1990 年江西省小学生“八一杯”数学比赛题)解：

　　(1)“减去 1 能被 2 整除”的数，可知这个数是奇数。

　　(2)“减去 2 能被 5 整除”的数，可知它的个位数是 2 或 7。

　　(3)“减去 3 能被 7 整除”的数，可知这个数是 10、 17、24、⋯⋯ 同时符合(1)、(2)、(3)的数是 17。

　　因为 2、5、7 的最小公倍数是 70，所以同时符合(1)、(2)、 (3) 的数的一般式是 70×n+17。

　　又因为“一个数加上 4 能被 9 整除”相当于“一个数被 9 除不足 4”， 也就是“一个数被 9 除余 9-4=5”。所以用 n=1、2、3、4、5、⋯⋯代入 70×n+17，当 n=6 时，70×6+17=437 被 9 除余 5，由此得符合题意的最小数是437。

　　答：这个数最小是 437。

　　例 10 幼儿园拿出一块长方体木料，长 72 厘米，宽 60 厘米，高 36 厘

　　米，请王师傅把它锯成同样大小的正方体木块，木块的体积要最大，木料又不能剩余，算一算，可以锯成几块?

　　(厦门市小学生 1986 年“从小爱数学”预赛题) 解：由题意可得王师傅要把原长方体木料锯成同样大小的正方体木块(体积要最大)，木料又不能剩余，那么锯成的正方体的棱长必须是长方体木料的长、宽、高的最大公约数。

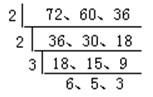
　　72、60、36 的最大公约数是 2×2×3=12。所以，能锯成最大正方体的木块数是 6×5×3=90(块)。或(72×60×36)÷(12×12×12)90(块)。 答：可以锯成 90 块。

编辑推荐：

小升初奥数各知识点详细解析汇总

四大名校小升初择校考之奥数解题攻略

2012小升初奥数总复习资料