奥数题及答案：

　　学而思奥数天天练栏目每日精选中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考题学习经历，并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点，适合一些志在竞赛中夺取佳绩的学生。

　　·本周试题由学而思奥数名师精选、解析，以保证试题质量。

　　·每周末，我们将一周试题汇总为word版本试卷，您可下载打印或在线阅读。

　　·每道题的答题时间不应超过15分钟。答案明日公布！

　　【最短路线问题】

　　1.难度：★★★★

　　图4-4是一个街道的平面图，纵横各有5条路，某人从A到B处（只能从北向南及从西向东），共有多少种不同的走法？

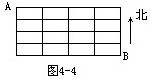
　　【分析】因为B点在A点的东南方向，题目要求我们只能从北向南及从西向东，也就是要求我们走最短路线。解：如图所示。

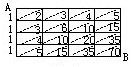
　　答：从A到B共有70种不同的走法。
 

　　2.难度：★★★★★

　　如图4-6，从甲地到乙地最近的道路有几条？

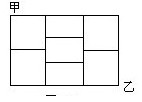
　　【分析】

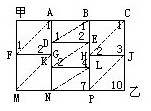
    求从甲地到乙地最近的道路有几条，也就是求从甲地到乙地的最短路线有几条.把各交叉点标上字母，如图4-7.这道题的图形与例1、例2的图形又有所区别，因此，在解题时要格外注意是由哪两点的数之和来确定另一点的。

　　①由甲→A有1种走法，由甲→F有1种走法，那么就可以确定从甲→G共有1＋1＝2（种）走法。

　　②由甲→B有1种走法，由甲→D有1种走法，那么可以确定由甲→E共有1+1＝2（种）走法.

　　③由甲→C有1种走法，由甲→H有2种走法，那么可以确定由甲→J共有1+2=3（种）走法。

　　④由甲→G有2种走法，由甲→M有1种走法，那么可以确定从甲→N共有2＋1=3（种）走法。

　　⑤从甲→K有2种走法，从甲→E有2种走法，那么从甲→L共有2＋2=4（种）走法。

　　⑥从甲→N有3种走法，从甲→L有4种走法，那么可以确定从甲→P共有3＋4=7（种）走法。

　　⑦从甲→J有3种走法，从甲→P有7种走法，那么从甲→乙共有3+7=10（种）走法。

　　解：在图4-7中各交叉点标上数，乙处标上10，则从甲到乙共有10条最近的道路。