答　案

　　如图所示：

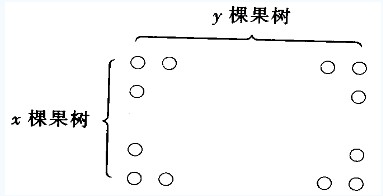
　　根据{（1）果树林的果树都成行排列，每片果树林中各行的果树棵数相等。}，设{（3）有三片果树林，每片果树林四周边界上的果树与其内部的果树棵数相等。}中提到的三片果树林的两条相邻边上果树的棵数分别为x和y.于是边界上果树的棵数等于（y+y）+（x-2）+（x-2），即2y+2x-4；而内部果树的棵数等于（x-2）×（y-2）根据{（3）有三片果树林，每片果树林四周边界上的果树与其内部的果树棵数相等。}，

　　2y+2x-4=（x-2）（y-2）

　　解出x，

　　于是y必须大于4，而y-4必须整除4y-8。

　　经反复试验，得出以下四对数值：

　　x y

　　________________________

　　12 5

　　8 6

　　6 8

　　5 12

　　（这里是全部可能的数值，因为（4y-8）/（y-4）等于4+8/（y-4），要使8/（y-4）为正整数，y必须是5、6、8或者12。）

　　根据{（2）苹果林的行数最少，柠檬林比苹果林多一行。柑橘林比柠檬林多一行，桃树林又比柑橘林多一行。}，一定是苹果林有5行，柠檬林有6行，柑橘林有7行，桃树林有8行。

　　由于有7行果树的柑橘林不能满足条件（3），所以边界上的果树与内部的果树棵数不相等的果树林是柑橘林。