（2010年第8届希望杯1试第6题）

　　6.某校的学生的属相有鼠、牛、龙、蛇、马、羊、猴、鸡、狗、猪。那么至多选出___________位学生，就一定能找到属相相同的两位学生。

　　【答案】11

　　【解析】有10种属相，10＋1＝11人就可以满足条件。

　　（2010年第8届希望杯1试第7题）

　　7.某养鸡场的母鸡只数是公鸡只数的6倍，后来公鸡、母鸡各增加60只，母鸡的只数变为公鸡只数的4倍，则养鸡场原来一共养了___________只鸡。

　　【分析】要保持母鸡是公鸡的6倍，母鸡增加60，公鸡就要增加360，所以360－60＝300就是差的2倍，现在有150只母鸡，原来有90只母鸡，一共养了630只鸡。

　　（2010年第8届希望杯1试第8题）

　　8.将几个大小相同的正方体木块放成一堆，从正面看到的视图是图（a），从左向右看到的视图是图（b），从上向下看到的视图是图（c），则这堆木块最多共有___________块。

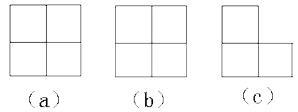
　　【答案】6

　　【解析】对于图c来说，每个小方块都摞了2层，最多有6块。

　　（2010年第8届希望杯1试第9题）

　　9.将边长为10厘米的五张正方形纸片如图那样放置，每张小正方形纸片被盖住的部分是一个较小的正方形，它的边长是原正方形边长的一半，则图中的图形外轮廓（图中粗线条）的周长为___________厘米。

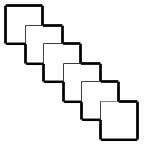
　　【答案】120

　　【解析】可以把图形平移扩大成为边长30厘米的大正方形，周长不变，所以周长是30×4＝120厘米。

　　（2010年第8届希望杯1试第10题）

　　10.几百年前，哥伦布发现美洲新大陆，那年的年份的四个数字各不相同，它们的和等于16，如果十位数字加1，则十位数字恰等于个位数字的5倍，那么哥伦布发现美洲新大陆是在公元___________年。

　　【答案】1492

　　【解析】肯定是1×××年，16－1＝15，百位，十位与个位和是15，十位加1后，数字和是15＋1＝16，此时十位和个位和是6的倍数，个位不是1，只能是2，十位原来是9，百位是4，所以是在1492年。