97.最少有几个座位？

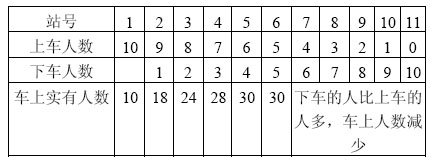
　　有一条公共汽车的行车路线，除去起始站和终点站外，中途有9个车站。

　　一辆公共汽车从起始站开始上乘客，除终点站外，每一站上车的乘客中，都恰好各有一位乘客从这一站到以后的每一站。为了使每位乘客都有座位，这辆公共汽车至少要有多少个座位？

　　分析与解 中途有9个车站，加上终点站共10个车站。根据题意，在起始站上车的有10个人，在这10人中以后每站都有1人下车；在第二站上车的9人，在这9人中，以后每站下去1人。在起始站上车的有1人在第二站下车，于是在第二站至第三站之间汽车上实有10＋9-1=18（人）。这样推算下去，列表如下：

　　98.将军饮马

　　古希腊一位将军要从A地出发到河边（如下图MN）去饮马，然后再回到驻地B.问怎样选择饮马地点，才能使路程最短？

　　100.有名的牛吃草的问题

　　牛顿的名著《一般算术》中，还编有一道很有名的题目，即牛在牧场上吃草的题目，以后人们就把这种应用题叫做牛顿问题。

　　“有一片牧场的草，如果放牧27头牛，则6个星期可以把草吃光；如果放牧23头牛，则9个星期可以把草吃光；如果放牧21头牛，问几个星期可以把草吃光？”

　　解答这道题时，我们假定牧草上的草各处都一样密，草长得一样快，并且每头牛每星期的吃草量也相同。

　　你会解这道题吗？

　　分析与解 在牧场上放牛，牛不仅要吃掉牧场上原有的草，还要吃掉牧场上新长出的草。因此解答这道题的关键是要知道牧场上原有的牧草量和每星期草的生长量。

　　设每头牛每星期的吃草量为1，则27头牛6个星期的吃草量为27×6=162，这既包括牧场上原有的草，也包括6个星期长的草。

　　23头牛 9个星期的吃草量为 23×9= 207，这既包括牧场上原有的草，也包括9个星期长的草。

　　因为牧场上原有的草量一定，所以上面两式的差207-162=45正好是9个星期生长的草量与6个星期生长的草量的差。由此可以求出每星期草的生长量是45÷（9-6）=15.牧场上原有的草量是162-15×6=72，或207-15×9= 72.前面已假定每头牛每星期的吃草量为1，而每星期新长的草量为15，因此新长出的草可供15头牛吃。今要放牧21头牛，还余下21-5=6头牛要吃牧场上原有的草，这牧场上原有的草量够6头牛吃几个星期，就是21头牛吃完牧场上草的时间。72÷6=12（星期）。

　　也就是说，放牧21头牛，12个星期可以把牧场上的草吃光。