第二届小学“新知杯”第1讲漫谈整除(4)
上海奥数网
2011-10-19 13:30:52
1、（第二届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛团体对抗题）一个自然数N乘以13后，后三位是579。N最小是多少？
2、（列宁格勒数学奥林匹克）应当在如下的问号（?）的位置上填上哪一个数码，才能使得所得的整数可被7整除？（其中数码6和5各重复了50次）666.66?555.55
3、（2009年第十届“中环杯”小学生思维能力训练活动五年级选拔赛）一个七位数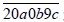
是33的倍数，那么a.b.c._______。
4、（2010年第九届“小机灵杯”小学数学竞赛（复赛）试题）将数字0，1，2，3，4，5各使用一次，组成一个能被667整除的六位数，那么，这个六位数除以667的结果是________。
5、（2010年首届“新知杯”沪港少年数学邀请赛第二试）用1，2，3，4，6，7，8，9这八个数字中的若干个可以组成许多个能被99整除的数。其中最小的数是_______，最大的数是_______。
6、（2007年台湾第十一届小学数学世界邀请赛个人赛）有一个九位数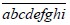
的各位数字都不相同且全都不为0，并且二位数
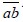可被2整除，三位数
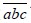可被3整除，四位数
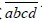可被4整除……以此类推，九位数
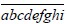可被9整除。请问这个九位数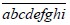是什么？
