(10×2+4)÷(10-8)=12(间)

　　8×12+4=100(头)

　　或10×12-10×2=100(头)

　　▍解题方法10——假设

　　小华解答数学判断题，答对一题给4分，答错一题扣4分，她答了20道判断题，结果只得56分。小华答对了几题？

　　假设小华全部答对：该得4×20=80(分)，

　　现在实际只得了56分，相差80-56=24(分)，

　　因为答对一题得4分，答错一题扣4分，这样，一对一错相比，一题就差8分(4+4=8)，

　　根据总共相差的分数以及做错一题相差的分数，就可以求出做错的数：24÷8=3(题)，

　　一共做20题，答错3题，答对的应该是：

　　20-3=17(题)

　　4×17=68(分)(答对的应得分)

　　4×3=12(分)(答错的应扣分)

　　68-12=56(分)(实际得分)

　　某校有100名学生参加数学竞赛，平均得63分，其中男生平均得60分，女生平均得70分，那么，男生比女生多多少名？

　　假设100名同学都是男生，那么应得分

　　60×100=6000(分)

　　比实际少得

　　63×100-6000=300(分)

　　原因是男生平均分比女生少

　　70-60=10(分)

　　求出女生人数为

　　300÷10=30(名)

　　▍解题方法11——转化

　　数学题常用的也是十分重要的一种方法——转化。这种转化通常是指转化条件或问题，特别是转化题中的数量关系。

　　巧妙转化：在解奥数题时，经常要提醒自己，遇到的新问题能否转化成旧问题解决，化新为旧，透过表面，抓住问题的实质，将问题转化成自己熟悉的问题去解答。转化的类型有条件转化、问题转化、关系转化、图形转化等。

　　两个数相除的商是21，余数是3。如果把被除数、除数、商和余数相加，它们的和是225。被除数、除数各是多少？

　　题目中前一句话换个说法就是：被除数比除数的21倍还多3。再换个说法就是：被除数与除数的和比除数的“21+1”倍还多3。

　　题目中第二句话换个说法是：被除数与除数的和是225-(21+3)=201。

　　整个题目的意思换个说法就是：201比除数的22倍多3。

　　从而可以先求出除数是：(201-3)÷22=9

　　可求出被除数是：21×9+3=192

　　▍解题方法12——抓“不变量”

　　数学题中，常常会出现数量的增减变化，但这些量变化时，与它们相关的另外一些量却没有改变。这种“不变量”往往在分析数量关系时起到重要作用。

　　今年小明8岁，小强14岁。几年后小明和小强岁数的和是40岁？

　　从年龄上不变来找解题的“突破口”

　　小明和小强的年龄差是：14-8=6(岁)

　　小明那一年是：(40-6)÷2=17(岁)

　　是在几年之后呢？17-8=9(年)

　　王进和张明计算甲、乙两个自然数的积(这两个自然数都比1大)。王进把甲数的个位数字看错了，计算结果为91，张明却把甲数的十位数字看错了，计算的结果为175。两个数的积究竟是多少？

　　91=7×13=1×91，所以175和91的公约数是1或7，因为乙数比1大，所以乙数一定是7。

　　抓住：一个因数(乙数)没有变，乙是91和175的公约数

　　91÷7=13……王进看错了的甲数

　　175÷7=25……张明看错了的甲数。

　　15×7=105

　　▍解题方法13——找隐蔽条件

　　应用题中的隐蔽条件，往往是分析问题的突破口或者是最关键的一步。所以，审题时如果感到缺少条件，你不妨提醒自己：有没有什么隐蔽条件？

　　一个家庭由丈夫、妻子、女儿和儿子组成，他们的年龄和是73岁。丈夫比妻子大3岁，女儿比儿子大2岁。4年前这个家庭成员的年龄和是58岁。请问：这个家庭成员现在的年龄各是多少岁？

　　隐蔽条件，可以推知：儿子今年才3岁。

　　（由题意：73-58=15（岁），4×4=16由此可知儿子4年前未出生，

　　又因相差一岁，所以儿子3岁．）

　　由“女儿比儿子大2岁”可以算出女儿今年是：3+2=5(岁)

　　从而可知，丈夫与妻子现在的年龄和是：

　　73-(5+3)=65(岁)

　　由他们的年龄差是3岁，容易算出丈夫今年是：

　　(65+3)÷2=34(岁)

　　妻子今年是：65-34=31(岁)

　　点评：解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的数量关系，再求解．

　　一个等腰三角形的周长是24厘米，其中有一条边长是6厘米，求另外两条边的长？

　　答：等腰三角形的腰不能是6厘米，所以只能底是6厘米另两条边：(24-6)÷2=9(厘米)

　　6厘米

　　▍解题方法14——整体看问题

　　从整体上观察思考，全面地审题。

　　整体把握：有些奥数题，如果从细节上考虑，很繁杂，也没有必要。如果能从整体上把握，宏观上考虑，通过研究问题的整体形式、整体结构、局部与整体的内在联系，“只见深林，不见树木”，来求得问题的解决。

　　有甲、乙、丙三种货物。如果买甲3件，乙7件，丙1件，共花去3.15元；如果买甲4件，乙10件，丙1件，共花去4.20元。现在买甲、乙、丙各1件，需要花多少钱？

　　买甲3件，乙7件，丙1件，花3.15元①

　　买甲4件，乙10件，丙1件，花4.20元②

　　要想求出买甲1件，乙1件，丙1件，共需花多少钱，必须使上述①与②中对应的“件数”相差1。

　　为此，可转化已知条件：

　　将条件①中的每个量都扩大3倍，得：

　　买甲9件，乙21件，丙3件，花9.45元③

　　将条件②中的每个量都扩大2倍，得：

　　买甲8件，乙20件，丙2件，花8.40元④

　　所以，买甲、乙、丙各一件，共需要花的钱数为

　　9.45-8.40=1.05(元)

　　一条马路长2000米，老张在马路的一端，老李在马路的另一端。他们分别从这条马路的两端同时出发，相对而行。老张每分钟走60米，老李每分钟走40米。老张带着一条狗，狗每分钟跑120米。这条狗与老张一同出发，碰到老李时就向老张跑，碰到老张又向老李跑，……直到老张与老李相遇。问这条狗从出发到老张与老李相遇时共跑了多少米？

　　提示：不需要把狗每趟所跑的路分别算出来，只要用它的速度乘一共所跑的时间就可以了。

　　▍解题方法15——分情况讨论

　　对于那些缺少条件，看上去无法回答的问题，经过全面深入的思考，分几种情况来讨论，是可以找到问题的完整(全部)答案的。

　　甲地到乙地的公路长400千米，两辆汽车从两地同时出发对开，甲车每小时行38千米，乙车每小时行42千米。出发几小时后两车相距80千米？

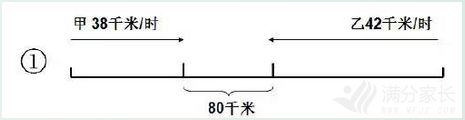
　　(400-80)÷(38+42)

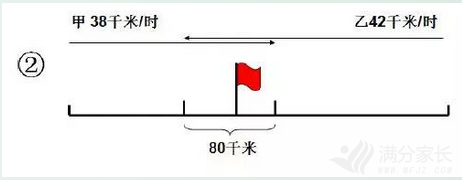
　　(400+80)÷(38+42)

　　在连续的49年中，最多可以有多少个闰年？最少应该有多少个闰年？

　　49年中有几个4年，一般就有几个闰年

　　在通常情况下，连续49年中有12个闰年。

　　49年必须是连续的。但它没有规定这49年的起止时间。

　　但，当第一年是闰年时，最后一年也正好是闰年。

　　把一根竹竿垂直插入水中，在竹竿上刻上一个记号表示水深；再把这根竹竿掉过头来插入水中，也刻上一个记号表示水深。已知两个记号相距10厘米，是水深的十分之一。求竹竿的长。

　　一种：水深：10×10=100(厘米)

　　竿长：100+100+10=210(厘米)

　　另一种：水深：10×10=100(厘米)

　　竿长：100+100-10=190(厘米)

　　一根铁丝可以弯成长、宽分别是4厘米、3厘米的长方形。如果用这根铁丝弯成两个相同的正方形，每个正方形面积是多少？

　　(4+3)×2=14(厘米)

　　14÷8=1.75(厘米)1.75×1.75=3.0625(平方厘米)

　　(4+3)×2=14(厘米)

　　14÷7=2(厘米)2×2=4(平方厘米)

　　▍解题方法16——逐步调整

　　你可以根据题中的部分条件，找到一个与正确答案比较接近的“准答案”，然后再对它进行修改或调整。这样一步一步地逼近，最后一定会得到符合题中所有条件的正确答案的。

　　▍解题方法17——合理变形

　　把算式合理变形，是我们进行简便计算最常用的方法。例如：99×99+199

　　合理的变形可以使解题过程变得简捷而灵活。怎样的变形才是“合理”的呢？

　　(1)题目变形之后，要使隐蔽的简算特点暴露出来；

　　(2)只能变“形”，而不能改变数的大小。

　　▍解题方法18——用字母表示数

　　方方、圆圆、丁丁、宁宁四个小朋友共有45本书，但是不知道每人各有几本书。如果变动一下：方方的减少2本，圆圆的增加2本，丁丁的增加一倍，宁宁的减少一半，那么四个小朋友的书就一样多。问：每个小朋友原来各有几本书？

　　解：设一样多是x本。

　　X+2+X-2+X÷2+2X=45

　　X=10

　　方方：10+2=12丁丁：10÷2=5

　　圆圆：10-2=8宁宁：2X=20

　　▍解题方法19——借来还去

　　我国民间流传着这样一个故事，一位老人临终时决定把家里的17头牛全部分给三个儿子。其中大儿子分得二分之一，二儿子分得三分之一，小儿子分得九分之一，但不能把牛杀掉或卖掉。三个儿子按照老人的要求怎么也不好分。后来一位邻居用“借来还去”法顺利地把17头牛分完了。

　　某汽水厂规定：用3个空汽水瓶可换一瓶汽水，某人买了10瓶汽水，问他总共可喝到几瓶汽水？

　　如果3个空瓶可换1平汽水，那么有2个空瓶就可喝到1瓶汽水。这是因为：

　　有了2个空瓶，再到别人那里“借来”1个空瓶，就可换来1瓶汽水，喝完把空瓶给别人“还去”，这时不欠不余。

　　10瓶汽水喝完后得到10个空瓶，10个空瓶又可换来5瓶汽水，总共可喝到“10+5=15”瓶汽水。