备考杯赛2016华杯赛、迎春杯、希望杯三大杯赛即将开启，初赛时间进入倒计时，小伙伴们要抓紧时间备考啦！

　　干货来袭19种速成解题法

　　★解题方法1——分类

　　★解题方法2——化大为小找规律

　　★解题方法3——把未知量具体化

　　★解题方法4——试验

　　★解题方法5——移多补少

　　★解题方法6——等量代换

　　★解题方法7——画图

　　★解题方法8——反过来想

　　★解题方法9——分析因果关系

　　★解题方法10——假设

　　★解题方法11——转化

　　★解题方法12——抓不变量

　　★解题方法13——找隐蔽条件

　　★解题方法14——整体看问题

　　★解题方法15——分情况讨论

　　★解题方法16——逐步调整

　　★解题方法17——合理变形

　　★解题方法18——用字母表示数

　　★解题方法19——借来还去

　　▍解题方法1——分类

　　分类是一种很重要的数学思考方法，特别是在计数、数个数的问题中，分类的方法是很常用的。

　　可分为这样几类：

　　(1)以A为左端点的线段共4条，分别是：AB，AC，AD，AE；

　　(2)以B为左端点的线段共3条，分别是：BC，BD，BE；

　　(3)以C为左端点的线段共2条，分别是：CD，CE；

　　(4)以D为左端点的线段有1条，即DE。

　　一共有线段4+3+2+1=10(条)。

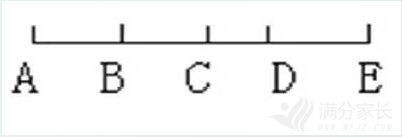
　　还可以把图中的线段按它们所包含基本线段的条数来分类。

　　(1)只含1条基本线段的，共4条：AB，BC，CD，DE；

　　(2)含有2条基本线段的，共3条：AC，BD，CE；

　　(3)含有3条基本线段的，共2条：AD，BE；

　　(4)含有4条基本线段的，有1条，即AE。

　　有长度分别为1、2、3、4、5、6、7、8、9、10、11(单位：厘米)的木棒足够多，选其中三根作为三条边围成三角形。如果所围成的三角形的一条边长为11厘米，那么，共可围成多少个不同的三角形？

　　提示：要围成的三角形已经有一条边长度确定了，只需确定另外两条边的长度。

　　设这两条边长度分别为a，b，那么a，b的取值必须受到两条限制：

　　①a、b只能取1～11的自然数；

　　②三角形任意两边之和大于第三边。

　　1、11一种

　　2、112、10二种

　　3、113、103、9三种

　　4、114、104、94、8四种

　　5、115、105、95、85、7五种

　　6、116、106、96、86、76、6六种

　　7、117、107、97、87、7五种

　　8、118、108、98、8四种

　　9、119、109、9三种

　　10、1110、10二种

　　11、11一种

　　1+2+3+4+5+6+5+4+3+2+1=36种

　　▍解题方法2——化大为小找规律

　　对于一些较复杂或数目较大的问题，如果一时感到无从下手，我们不妨把问题尽量简单化，在不改变问题性质的前提下，考虑问题最简单的情况(化大为小)，从中分析探寻出问题的规律，以获得问题的答案。这就是解数学题常用的一种方法，叫做归纳，我们也可以叫做“化大为小找规律”。

　　10条直线最多可把一个长方形分成多少块？

　　提示：先不考虑10条直线，而是先看1条、2条、3条直线能把一个长方形分成几块？

　　10条直线最多可把一个长方形分成多少块？

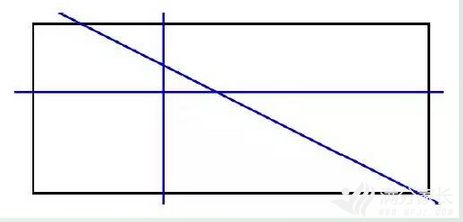
　　第一条直线：分成2块

　　第二条直线：分成2+2=4块

　　第三条直线：分成2+2+3=7块

　　我们发现这样的规律：

　　=2+(2+3+4+5+6+7+8+9+10)

　　=2+54

　　=56(块)

　　这就是说，10条直线可把长方形分为56块。

　　▍解题方法3——把未知量具体化

　　一般情况下，题目中的未知量不可以随便假设。有时，问题中所求的未知量与其它相关的未知量具体是多少并没有关系。在这种情况下，可以把这些没有关系的未知量设为具体数。”

　　在减法中，被减数、减数、差相加的和，除以被减数，所得的商是多少？

　　幼儿园把一筐苹果平均分给大班和小班的小朋友，每个小朋友可分得6个。如果全部分给大班小朋友，那么平均每人可分10个。如果全部分给小班的小朋友，平均每人可分几个？

　　全部分给小班的小朋友，每人可分几个，与苹果的总个数有关系，而与人数(无论是两班人数，还是大班人数)都没有关系。

　　苹果总数=两班总人数×6

　　苹果总数=大班人数×10

　　所以，大班人数×10=两班总人数×6

　　设两班100人大班100×6÷10=60人

　　小班100-60=40人600÷40=15个

　　▍解题方法4——试验

　　将一根长为374厘米的铝合金管截成若干根长36厘米和24厘米的短管。问剩余部分的管子最少是多少厘米？

　　提示：从题目的问句看，应抓住“最少”二字来思考，先考虑没有剩余，再考虑剩余1厘米、2厘米……

　　(1)如果把这根长管截成若干根两种不同规格的短管后没有剩余，那么374应该是4的倍数，因为两种短管的长度36厘米、24厘米都是4的倍数，但374不能被4整除，所以没有剩余不可能。

　　(2)如果截成若干根两种不同规格的短管后只剩下1厘米，根据36、24都是偶数，“偶数的倍数是偶数”、“偶数与偶数的和是偶数”可推知，原来铝合金管长应为奇数，这与管长374(偶数)的条件矛盾，所以，剩1厘米也不可能。

　　(3)如果最后剩下2厘米。这种情况有可能。374÷(36+24)=6……14。这说明两种都截6根余14厘米，这时需要调整：少截一根24厘米长的，加上14，24+14=36+2，正好合一根36厘米长的，还剩2厘米。

　　另外，枚举法：奥数题中常常出现一些数量关系非常特殊的题目，用普通的方法很难列式解答，有时根本列不出相应的算是来。我们可以用枚举法，根据题目的要求，一一列举基本符合要求的数据，然后从中挑选出符合要求的答案。

　　▍解题方法5——移多补少

　　在“平均”二字中，“平”就是“拉平”，也就是移多补少，“均”就是相等。“平均”二字的意思，通俗地说，就是用“移多补少”的办法，使每份数量都相等。因此，移多补少是我们解答求平均数应用题的重要思考方法。

　　新光机器厂装配拖拉机，第一天装配50台，第二天比第一天多装配5台，第三、第四两天装配台数是第一天的2倍多3台，平均每天装配多少台？

　　用四天装配总台数除以4，综合算式为：[50+(50+5)+(50×2+3)]÷4=52(台)

　　采用移多补少的方法，假设每天都装配50台，那么四天一共多装配5+3=8(台)，把这8台平均分成四份，8÷4=2(台)，

　　因此，平均每天装配50+2=52(台)

　　综合算式为：50+(5+3)÷4=52(台)

　　甲、乙、丙三人一起买了8个面包，平均分着吃，甲拿出5个面包的钱，乙付了3个面包的钱，丙没带钱，等吃完后一算，丙应该拿出4角钱，问甲应收回多少钱？(以分为单位)

　　4角=40分

　　40×3=120(分)

　　120÷8=15(分)

　　15×5-40=35(分)

　　▍解题方法6——等量代换

　　“曹冲称象”是运用了“等量代换”的思考方法：两个完全相等的量，可以互相代换。解数学题，经常会用到这种思考方法。

　　百货商店运来300双球鞋，分别装在2个木箱、6个纸箱里。如果2个纸箱同1个木箱装的球鞋一样多，每个木箱和每个纸箱各装多少双球鞋？

　　提示：我们根据“2个纸箱同一个木箱装的球鞋一样多”，把木箱换成纸箱，也就是说，把300双球鞋全部用纸箱装，不用木箱装。根据已知条件，2个木箱里的球鞋刚好装满4个纸箱，再加上原来已装好的6个纸箱，一共是10个纸箱。这样，题目就变为“把300双球鞋平均装在10个纸箱里，平均每个纸箱装多少双球鞋？”可以求出每个纸箱装多少双球鞋。也就能求出一个木箱装多少双球鞋。

　　用两台水泵抽水，小水泵抽6小时，大水泵抽8小时，一共抽水312立方米。小水泵5小时的抽水量等于大水泵2小时的抽水量，两种水泵每小时各抽水多少立方米？

　　5小=2大大换小：8÷2×5=20(时)

　　小：312÷(20+6)=12(立方米)

　　大：12×5÷2=30(立方米)

　　▍解题方法7——画图

　　在数学中，“数”与“形”就像一对形影不离的亲兄弟。几乎所有的数量关系或数学规律都可以用生动形象的示意图来反映。

　　A、B、C、D与小青五位同学一起比赛象棋，每两人都要比赛一盘。到现在为止，A已经赛了4盘，B赛了3盘，C赛了2盘，D赛了1盘。问小青已经赛了几盘？

　　A已经赛了4盘 B赛了3盘 C赛了2盘 D赛了1盘

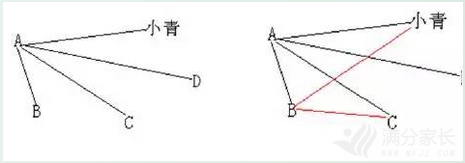
　　小青已经赛了2盘

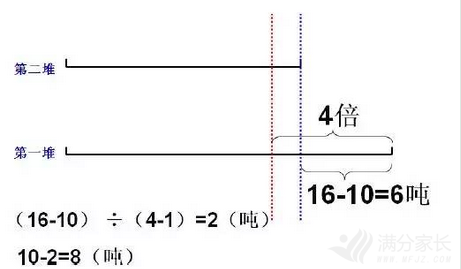
　　两堆煤，第一堆16吨，第二堆10吨，5天内两堆煤烧掉同样多吨数，这样第一堆剩下的煤正好是第二堆所剩煤的4倍。问5天中两堆煤被烧掉了多少吨？

　　▍解题方法8——反过来想

　　当你按习惯思路解决问题困难时，不妨也反过来想想。反过来想，是我们解数学题的一种很好的方法。

　　正难则反：有些数学问题如果你从条件正面出发考虑有困难，那么你可以改变思考的方向，从结果或问题的反面出发来考虑问题，使问题得到解决。

　　用淘汰制比赛从200名乒乓球选手中产生一名冠军，问应进行多少场比赛？

　　淘汰199人需要比赛199场

　　1至100的自然数中，不能被9整除的自然数的和是多少？

　　从1至100的和中去掉9的倍数，就是不能被9整除的数的和了

　　1+2+3+。。。+100=5050

　　9×(1+2+3+…+11)=594

　　5050-594=4456

　　另外，倒推法：从题目所述的最后结果出发，利用已知条件一步一步向前倒推，直到题目中问题得到解决。

　　▍解题方法9——分析因果关系

　　分析，也就是抓住结果找原因。我们解数学题，也应当学会这种顺藤摸瓜，分析因果关系的本领。

　　用一个杯子向一个空瓶里倒水。如果倒进3杯水，连瓶共重440克。如果倒进5杯水，连瓶共重600克。一杯水和一个空瓶各重多少？

　　我们先把两次倒水的情况作一次比较。

　　从连瓶重量来看，第二次比第一次重了

　　“600-440=160(克)”，

　　怎么会多160克的呢？因为第二次比第一次多倒了“5-3=2(杯)”水。

　　这样，我们就容易求出每杯水的重量为：160÷2=80(克)。

　　空瓶重量600-80×5=200(克)

　　这类应用题的一般思路：

　　(1)先比较两种情形，从数量上看出差别；

　　(2)分析造成这种数量差别的原因；

　　(3)利用这种因果关系来沟通题目中已知量与未知量的关系，并求出正确答案。

　　兴旺养猪场，如果每间猪圈养猪8头，就还有4头猪没有猪圈养；如果每间猪圈养猪10头，将空出2间猪圈。问这个养猪场有多少间猪圈？共养了多少头猪？

【点击下页查看更多】