9、（10分）图中长方形内画了一些直线，已知边上有三块面积分别是15，34，47，求图中阴影部分的面积是多少。

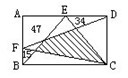
　　解析：一半模型

　　答案：15+34+47=96

　　10、（10分）将440拆分为11个自然数的和，使这11个自然数从小到大排成一行后，相邻两个数的差都是５.求第１个数和第９个数分别是几？

　　解析：数论问题

　　设最小的那个数为a，则这11个自然数分别为：a、a+5、a+10、…、a+50

　　根据题意：11a+5*（1+2+3+…+10）=440

　　求得：a=15

　　所以第一个数：a=15   第9个数：15+5*8=55

　　11、（10分）某公司在A、B两地分别库存有某机器16台和12台，现要运往甲、乙两家客户的所在地，其中甲方15台，乙方13台。已知从A地运一台到甲方的运费为500元，到乙方的运费为400元，从B地运一台到甲方的运费为300元，到乙方的运费为600元。已知运费由公司承担，公司应设计怎样的调运方案，才能使这些机器的总运费最省？费用最少是多少？

　　解析：杂题统筹规划问题

　　B地机器全部运送到甲地：12*300=3600

　　A地机器分开运送，甲地3台：3*500=1500，乙地13台：13*400=5200

　　所以费用为：3600+1500+5200=10300（元）

　　12、（10分）一次数学竞赛，准备了22支铅笔作为奖品发给一、二、三等奖的学生，原计划发给一等奖每人6支，二等奖每人3支，三等奖每人2支，后来改为一等奖每人9支，二等奖每人4支，三等奖每人1支，总支数仍是22支。问：获一、二、三等奖的学生各多少名？

　　解析：求解不定方程

　　设一等奖x，二等奖y，三等奖z

　　6x+3y+2z=22①

　　9x+4y+z=22②

　　②×2－①得

　　12x＋5y＝22

　　x为整数只能为1

　　y=2  z=5

　　则一、二、三等奖的学生各有：1、2、5名。

　　13、（10分）甲、乙、丙三队要完成A、B两项工程。B工程的工作量比A工程的工作量多1/4。甲、乙、丙三队单独完成A工程所需要的时间分别是20天、24天、30天。为了同时完成这两项工程，先派甲队做A工程，乙、丙两队共同做B工程；经过几天后，又调丙队与甲队共同完成A工程。丙队与乙队合做了多少天？

　　解析：应用题工程问题

　　设乙丙合作a天。

　　求解a=15（天）

　　14、（10分）汽车在南北走向的公路上行驶时，由南向北逆风而行，每小时50千米；由北向南顺风而行，每小时行70千米。两辆汽车同时从同一地点出发相背而行，一辆汽车往北驶去然后返回，另一辆汽车往南驶去然后返回，结果4小时后，两车同时回到出发点。如果掉头时间不计，在这4小时内两车行驶的方向相同的有多少小时？

　　解析：行程问题

　　两辆汽车从出发点出发时速度比：5:7

　　两车相背而行路程分别为：5/12    7/12

　　路程差就是两车行驶方向相同：7/12-5/12=1/6

　　所以两车行驶方向相同的时间为：4*1/6=2/3

　　更多分享及讨论请点击查看：12月24日世界少年奥林匹克数学竞赛六年级试题

　　最后，预祝郑州小升初的同学们都能取得优异的成绩，进入理想的中学！

------------------------------------------------------------------------------------

　　编辑推荐：

　　决胜少儿数学邀请赛初赛真题及解析

　　决胜名校少儿数学邀请赛初赛现场报道

　　世界少年奥林匹克数学竞赛全解析

　　第十七届“华杯赛”25号开始网上报名