小升初奥数专题汇总之——牛吃草问题(一)
南京奥数网 来自家长帮社区的 @梁天祥老师 推出的奥数专题系列讲解好评如潮,小编整理了一下,供大家参考。
| 时钟问题(一) | 时钟问题(二) | 牛吃草问题(一) |
| 牛吃草问题(二) | 牛吃草问题(三) | 牛吃草问题(四) |
牛吃草问题简介:
“一堆草可供10头牛吃4天,那么这堆草可供8头牛吃几天?”
这个问题很简单,因为草的总量没有变,所以可以得到10×4÷8=5(天)。
但是,若问题中的“一堆草”改成“一片正在生长的草地”,问题就没有这么简单了,因为草的总量是在变化的。
像这类工作总量不固定但匀速增长的问题称为牛吃草问题。
举个例子:
牧场上有一片均匀生长的牧草,可供27头牛吃6周,或供23头牛吃9周。那么它可供21头牛吃几周?
这类问题最早出现在英国伟大的科学家牛顿所著的《普通算术》一书中,所以被后人称为“牛顿问题”,或“牛吃草”问题。
问题分析:
解答这类问题,困难在于草的总量在变,它每天、每周都在均匀地生长,时间越长,草的总量越多。
草的总量可以分成两个部分:(1)原有的草量;(2)某段时间内新生长的草量。
因此,必须设法找出这两个量来。
下面就以上面的题目为例进行分析。请看下图:
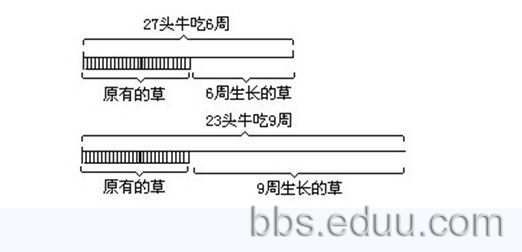
从上面的线段图可以看出23头牛9周的总草量比27头牛6周的总草量多,多出部分相当于3周新生长的草量。为了求出一周新生长的草量,就要进行转化。
我们假设1头牛1周吃掉的草量为1个单位,则:
27头牛6周吃掉的草量为27×6=162个单位;
23头牛9周吃掉的草量为23×9=207个单位。
这样一来,就可以知道每周生长的草量为:(207-162)÷(9-6)=15个单位。
进而,我们可以知道,原有草量为:27×6-15×6=72个单位(参考示意图)。
最后,我们来解决题目中提出的问题,这片草可供21头牛吃几周?







