备战2013年华杯赛历年精选真题讲解:多角度探索解题新思路(2)
华杯赛官网
2013-01-17 17:22:28
证明五:延长EC交AB于G,则四边形ADCG是□,∴CE=AD=GC,即C是EG中点.又CF∥GB,∴F是EB中点,结论得证.
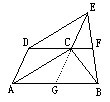
证明六:连结AE交CD于O点,则O 是AE中点,又OF∥AB,∴F是AB中点,得证.
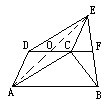
证明七:延长ED交BA延长线于H点,则HACD是□ , ∴CA=DH=ED ∴D是EH中点.又DF∥HB ∴F是EB中点,得证.
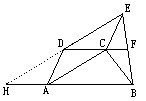
证明八:作ES∥CD交AD延长线于S,则CDSE是□ ∴DS=CE=AD ∴D是AS中点.又SE∥CD∥AB ∴F是EB中点,得证.
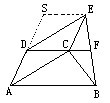
证明九:在证明一作的辅助线基础上,连结EQ,则可得ECBQ是□,从而F是□ECBQ对角线EB的中点。
总之,上述不同证法的辅助线可归结为以下两种:
①作平行线构成平行四边形和全等三角形进行等量代换。
②作平行线,由题设产生中点,通过平行线等分线段定理的推论得出结论。
这其中,其实蕴含了平面几何的平移变换和旋转变换的数学思想。
编辑推荐:









