2013年第十八届华罗庚金杯少年数学邀请赛(简称：华杯赛)备战已经开始了，为了让大家能够更好的为比赛做准备，宁波奥数网小编将历年的一些真题讲解整理出来，供大家。

　　例：如图，在梯形ABCD中，AB∥CD，四边形ACED是平行四边形，延长DC交BE于F.求证：EF=FB

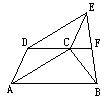
　　分析：这个题目本身不难，求证也容易，但通过对题设和结论的深入挖掘与探索，我们可以得出许多好的证法，总结如下：

　　证明一：如图所示，作BQ∥AD,交DF延长线于Q点，则四边形ABQD是平行四边形，从而BQ=AD，再由题设可证△CEF≌△QBF, 得证EF=FB.

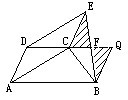
　　证明二：如左图所示：作FM∥DA交AB于M，则四边形ADFM是平行四边形，从而FM=DA.再证△CEF≌△MFB，从而结论可得证.

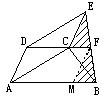
　　证明三：作CN∥EB交AB于N，则四边形CNBF是□，从而CN=FB.

　　再证：△ANC≌△DFE，可得CN=EF，即EF=FB.

　　证明四：作DP∥FB交AB于P，证明△ADP≌△CEF，从而得出结论.