例2：把一个多边形沿着几条直线剪开，分割成若干个多边形。分割后的多边形的边数总和比原多边形的边数多13条，内角和是原多边形内角和的1.3倍。请问：①原来的多边形是几边形?②把原来的多边形分割成了多少个多边形?

　　解：先来观察下面这组图形：

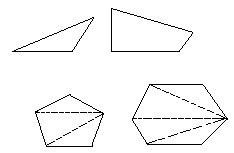
　　容易看出，n边形有n个顶点，n边形是由(n-2)个三角形组成的。因此，知道了一个多边形的边数或顶点数(n)，就可以求出它的内角和(n-2)×180°，知道了一个多边形由多少个三角形(m)组成的，就可以求出它的边数或顶点数(m+2)。

　　设原多边形是由a个三角形组成的，分割后的多边形共由b个三角形组成，a和b都是整数，根据题意有：

　　1.3×a×180°=b×180°，于是有1.3a=b。

　　由于b是整数，所以1.3a也是整数，a必是10的倍数，于是1.3a是13的倍数，b也是13的倍数。

　　(一)设a=10，则b=13，进而可知原多边形有12个顶点(12条边)，而分割后的多边形有15个顶点(15条边)。

　　由于连结一个多边形的两顶点时，将一个多边形分成两个多边形后，顶点的数目不变，而分出的两个多边形比原来增多2条边。连结多边形的一个顶点与一边上一点时，顶点数目增多1个，而分出的两个多边形比原来增多3条边。连接两边上一点时，顶点数目增多2个，而边数比原来增多4条。要增多(15-12=)3个顶点，增多13条边，有两种连线方法。(见下图)

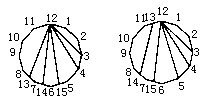
　　显然原多边形是12边形，两种连结方法都将12边形分成了6个多边形。

　　(二)如果a=20，则b=26，原多边形有22个顶点，而分割后的多边形有28个顶点，增多了(28-22=)6个顶点，不论怎样连结都不能使分割后的多边形边数总和比原来的多边形增多13条边。因此原多边形不是22边形。

　　如果a更大，则分割后增加的顶点个数更多，不论怎样连结都不符合题目要求。因此原多边形只能是12边形。

编辑推荐：

第十七届华杯赛网试初赛决赛试题汇总

第十七届华杯赛笔试决赛宁波赛区试卷及答案

备战2013华杯赛近五年题型难度及获奖率解析