和差倍分应用题占小升初试题的比重很大，尤其是分数应用题，虽然不是压轴题的难度，但还需格外重视，尤其是不能在这些熟悉的题目上浪费太多时间，通过训练，达到做此类题目又快又对的目的！

　　做分数应用题，方法很重要，现在我通过一道经典例题，简述一下目前试卷上主要体现的三种解法。

　　例题：一个装有彩球的口袋，红球占总数量的5/12，后来又放进27个红球，这时红球占现在总量的2/3，现在共有彩球多少个？

　　解法一：量率对应

　　步骤①：确定“单位1”

　　“单位1”一班来说是前后一直保持不变的量，对于这道题目来讲，红球前后有变化，那么总数前后也是改变的，但是其他颜色的球的数量没有变，所以这道题目就要把“其他的球”当做“单位1”

　　步骤②：转化分率

　　原来，红球占总数量的5/12，转化成红球占其他球的几分之几：红球5份，总数12份，其他球7份，则红球占其他球5/7。

　　现在，红球占总数量的2/3，转化成红球占其他球的几分之几：红球2份，总数3份，其他球1份，则红球是其他球的2倍。

　　步骤③：量率对应（对应量÷对应率=单位1）

　　题目中唯一的量是放入的27个球，也就是前后红球的变化量，那么对应的分率就是红球前后分率的变化

　　27÷（2－5/7）=21（个）——“单位1”，即其他球的数量

　　总量：21×2+21=63（个）

　　解法二：方程

　　方程的思路大多数都是从前往后正着想，开始不知道什么就设出来。

　　拿这道题来说：

　　①第一句话告诉了红球和总量的关系，但是具体多少个球不知道，所以可以把原来彩球总量设为x个（一般设单位1为x），则原来红球有5/12x个。

　　②红球放入27个后，现在有红球（5/12x＋27）个，总数变成（x+27）个。

　　③现在，红球占总数量的2/3，由此列出方程：5/12x+27=（x+27）×2/3，解得：x=36，现在总数：36+27=63（个）

　　解法三：画表格，巧填份数

　　①根据题意的两个分率转化成份数

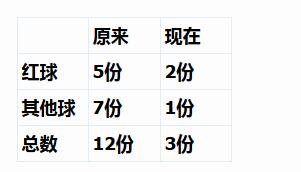
　　②不变量是“其他球”，但是其他球的份数前后不一样，再统一份数

　　③当“其他球”的前后份数统一后，所有份数对应的单位份数就都是一样的了，红球变化了27个，份数变化了14－5=9份

　　所以每份是27÷9=3（个），那么现在总数3×21=63（个）