2013陈省身杯必考点:计数问题模块
计数原理一般有两种类型,一个是几何计数,另一个是加乘原理。几何计数通常考察的是学生的图形思考方法和解题技巧,使学生容易因为疏忽或思考方法不当而造成错误。而加乘原理属于较难题目,在锻炼学生分类讨论思想的同时,还要求学生灵活掌握所学模型,对难题进行转换。
在陈杯考试中出现过的计数原理题目有:
(09年,第5题)数一数,下图中有几个不同的正方形?

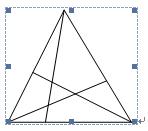
(11年,第5题)图中有几个三角形?
(08年,第16题)从0、0、1、2、3、4、5这七个数字中,任取三个组成三位数,可以组成多少个不同的三位数?
(11年,第14题)五张卡片上分别写有1、1、2、3、4用它们可以组成多少个不同的三位数?
(12年,第20题)唐老鸭、米老鼠和5个福娃贝贝、晶晶、欢欢、迎迎、妮妮站在一起,如果唐老鸭和米老鼠不能相邻,那么一共有多少种不同的站法?
一、几何计数问题,陈杯中多考察三角形的个数
针对这类问题,就要记住解题模型,然后再考虑转化难题。
如果有这样的图形,含有几个三角形?
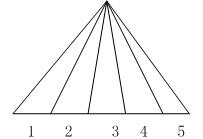
解决这样的问题,可以采用标号法,在相应线段上标号之后,就有5+4+3+2+1=15个三角形。掌握了这种方法,我们再看一道题。
【例1】下图中有几个三角形?
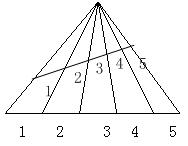
同样我们采用标号法,那么就有(5+4+3+2+1)+(5+4+3+2+1)=30个三角形。
熟悉这类模型可以帮助我们快速解题。同时遇到复杂的问题也可以向学过的模型靠拢。
【例2】下图中有几个三角形?
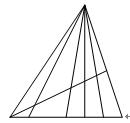
同样可以采用标号法,不过需要稍加变化。这时有15+15+5=35个三角形。
除此之外,我们还要熟练掌握拆线法。
【例3】下图中有几个三角形?(2011年陈杯)
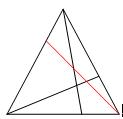
拆掉红线之后,有8个三角形。加上红线新形成了7个三角形。这样一共有15个三角形。
二、加乘原理问题
针对加乘原理的题目,就应该掌握分类讨论的思想。找到合适的分类原则,全面有序的进行分析。
【例4】从1到100的所有自然数中,不含4的自然数有多少个?
我们需要进行分类处理。分为一位数,两位数和三位数。
一位数不含4:有8种;
两位数不含4:先讨论十位上不含4有8种,个位上不含4有9种(包括0),这样就有8*9=72种;
三位数不含4:就一个数100;
这样就有81个数。
【例5】由数字1,2,3(不可重复使用)可以组成多少个没有重复的数字?
同样需要分类讨论。分为一位数,两位数和三位数。
一位数有3个;两位数有6个;三位数有6个;这样一共有15个数字。
【例6】五张卡片上分别写有1、1、2、3、4,用它们可以组成多少个不同的四位数?(2011年陈杯)
如果不取1没法构成4位数;如果取一个1,那么共有24;如果取两个1,那么我们先排列这两个1,固定一个1,找另外一个1的位置,有3种方法,而剩下的两个位置找两个数来填,有6个,这样一共有3*6=18种。那么一共有42个不同的四位数。
下面介绍一种新的方法,插空法。
没有1不能构成4位数;有一个1,我们要取其他三个数,这时会形成4个空位,把1填进这4个空位,有4*6=24;有两个1,我们取其他两个数,这时形成3个空位,把两个1填进这3个空位,有3*6=18。这样共有42个四位数。









