苏州奥数网讯：2012年第13届中环杯试题——五年级决赛试题如下，苏州奥数网整理试题及参考答案：

2012年第13届中环杯五年级决赛试题

　　1、我们有下列的公式:

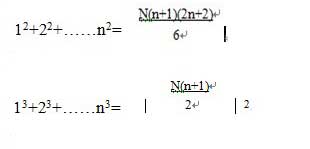
　　2、有一类四位数，除以5余1，除以7余4，除以11余9。这类四位数中最小的一个是几。

　　3、有A，B，C，D，E五个人，其中每个人永远说谎话或者永远说真话，并且他们彼此都互相知道对方的行为。A说B是说谎话者，B说C是说谎者，C说D是说谎者，D说E是说谎者。那么，这五个人中最多有几位说谎者。

　　4、在1-200之间有几个数，其所有不同的素因数之和为16（比如：12的所有不同的素因数为2，3，其和为2+3=5）。

　　5、某次数学比赛，计分方法有两种，分别是：第一种，答对一题给5分，答错不给分，不答给2分，第二种，先给39分，然后答对一题给3分，答错扣1分，不答不给分。某个考生完成所有题目后，用两种方法计分，都得71分。则这个考生未答得题目有几题。

　　6、在右图的数字谜中，每个字母代表了一个数字。不同的字母代表了不同的数字，相同的字母代表了相同的数字。则T=( )

　　7、平行四边形ABCD中，点P，Q，R，S分别为边AB，BC，CD，DA的中点，而点T为线段SR的中点。已知四边形ABCD的面积为120平方厘米，则三角形PQT面积为（ ）平方厘米。

　　8、已知一个筛子的六个面上分别写了六个不同的正整数，这六个正整数的和为60。现在对这个筛子进行这样的操作：每次操作选取正方体的一个顶点，将包含这个顶点的三个面上的数字都加1，经过多次的操作后，这个正方形的所有面上的数字都相同了。满足条件的不同的筛子有（ ）种（六个面的数字选定后就算一种，不考虑这六个数字如何放在筛子上）。

　　9、定义an=1+3+32+……3n(n为正整数），比如：a4=1+3+32+……34。那么a1,a2……a2013中，有（ ）各数是7的倍数。

　　10、如图所示，有一个边长为5厘米的立方体木块，在它的每个角以及每条棱和每个面的中间各挖去一个边长为1厘米的小立方体（即图中画有阴影的那些小立方体），那么余下部分的表面积是多少平方厘米？

下一页查看试题下载