1.有24个整数：

　　112、106、132、118、107、102、189、153、

　　142、134、116、254、168、119、126、445、

　　135、129、113、251、342、901、710、535。

　　问：当将这些整数从小到大排列起来时，第12个数是多少？

　　答案：134。

　　详解：粗略看一下，发现每个数字的百位所有数字均大于100。再仔细观察一下数字的百位和个位。首先，百位、十位分别为1和0的有3个数，百位、十位都为1的有5个数，百位、十位分别为1和2的有2个数。至此我们已经找到了10个数字，下面再看一下百位、十位分别为1和3的，它们是132、134、135。因此，第12个数应该是134。

　　2.一笔奖金分一等奖、二等奖和三等奖，每个一等奖的奖金是每个二等奖奖金的2倍，每个二等奖的奖金是每个三等奖金的2倍。如果评一、二、三等奖各两人，那么每个一等奖的奖金是308元；如果评一个一等奖、两个二等奖、三个三等奖，那么一等奖的奖金是多少元？

　　答案：392元。

　　详解：用图2-1的线段帮助我们说明题目中的奖金等级分配方案。

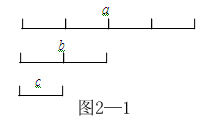
　　线段a表示一等奖的奖金数，线段b表示二等奖的奖金数，线段c表示三等奖的奖金数额。

　　根据题目中第一种假设的分配方式：

　　①一等奖2名，共获奖金308×2＝616（元）；

　　②二等奖2名，共获奖金（308÷2）×2＝308（元）；

　　③三等奖2名，共获奖金（308÷4）×2＝154（元）；

　　④奖金总额616＋308＋154＝1078（元）。

　　列综合算式如下：

　　308×2＋308＋308÷2＝1078（元）。

　　根据题中第二种假设的分配方式，画出示意图2-2。

　　如果把一个三等奖的奖金数看做一个单位，那么从图2-2可知：有三个单位的三等奖；两个二等奖奖金数相当于四个单位的三等奖奖金数；一个一等奖奖金数也和四个单位的三等奖奖金数目相同。

　　因此，每个三等奖奖金数目为：

　　1078÷（4＋4＋3）＝98（元）。

　　一等奖的奖金是：98×4＝392（元）。

　　列出综合算式：1078÷（4＋4＋3）×4＝392（元）。

　　3.已知

　　有24个整数：

　　112、106、132、118、107、102、189、153、

　　142、134、116、254、168、119、126、445、

　　135、129、113、251、342、901、710、535。

　　问：当将这些整数从小到大排列起来时，第12个数是多少？

　　答案：134。

　　详解：粗略看一下，发现每个数字的百位所有数字均大于100。再仔细观察一下数字的百位和个位。首先，百位、十位分别为1和0的有3个数，百位、十位都为1的有5个数，百位、十位分别为1和2的有2个数。至此我们已经找到了10个数字，下面再看一下百位、十位分别为1和3的，它们是132、134、135。因此，第12个数应该是134。

　　一笔奖金分一等奖、二等奖和三等奖，每个一等奖的奖金是每个二等奖奖金的2倍，每个二等奖的奖金是每个三等奖金的2倍。如果评一、二、三等奖各两人，那么每个一等奖的奖金是308元；如果评一个一等奖、两个二等奖、三个三等奖，那么一等奖的奖金是多少元？

　　答案：392元。

　　详解：用图2-1的线段帮助我们说明题目中的奖金等级分配方案。

　　线段a表示一等奖的奖金数，线段b表示二等奖的奖金数，线段c表示三等奖的奖金数额。

　　根据题目中第一种假设的分配方式：

　　①一等奖2名，共获奖金308×2＝616（元）；

　　②二等奖2名，共获奖金（308÷2）×2＝308（元）；

　　③三等奖2名，共获奖金（308÷4）×2＝154（元）；

　　④奖金总额616＋308＋154＝1078（元）。

　　列综合算式如下：

　　308×2＋308＋308÷2＝1078（元）。

　　根据题中第二种假设的分配方式，画出示意图2-2。

　　如果把一个三等奖的奖金数看做一个单位，那么从图2-2可知：有三个单位的三等奖；两个二等奖奖金数相当于四个单位的三等奖奖金数；一个一等奖奖金数也和四个单位的三等奖奖金数目相同。

　　因此，每个三等奖奖金数目为：

　　1078÷（4＋4＋3）＝98（元）。

　　一等奖的奖金是：98×4＝392（元）。

　　列出综合算式：1078÷（4＋4＋3）×4＝392（元）。

　　已知

　　有24个整数：

　　112、106、132、118、107、102、189、153、

　　142、134、116、254、168、119、126、445、

　　135、129、113、251、342、901、710、535。

　　问：当将这些整数从小到大排列起来时，第12个数是多少？

　　答案：134。

　　详解：粗略看一下，发现每个数字的百位所有数字均大于100。再仔细观察一下数字的百位和个位。首先，百位、十位分别为1和0的有3个数，百位、十位都为1的有5个数，百位、十位分别为1和2的有2个数。至此我们已经找到了10个数字，下面再看一下百位、十位分别为1和3的，它们是132、134、135。因此，第12个数应该是134。

　　一笔奖金分一等奖、二等奖和三等奖，每个一等奖的奖金是每个二等奖奖金的2倍，每个二等奖的奖金是每个三等奖金的2倍。如果评一、二、三等奖各两人，那么每个一等奖的奖金是308元；如果评一个一等奖、两个二等奖、三个三等奖，那么一等奖的奖金是多少元？

　　答案：392元。

　　详解：用图2-1的线段帮助我们说明题目中的奖金等级分配方案。

　　线段a表示一等奖的奖金数，线段b表示二等奖的奖金数，线段c表示三等奖的奖金数额。

　　根据题目中第一种假设的分配方式：

　　①一等奖2名，共获奖金308×2＝616（元）；

　　②二等奖2名，共获奖金（308÷2）×2＝308（元）；

　　③三等奖2名，共获奖金（308÷4）×2＝154（元）；

　　④奖金总额616＋308＋154＝1078（元）。

　　列综合算式如下：

　　308×2＋308＋308÷2＝1078（元）。

　　根据题中第二种假设的分配方式，画出示意图2-2。

　　如果把一个三等奖的奖金数看做一个单位，那么从图2-2可知：有三个单位的三等奖；两个二等奖奖金数相当于四个单位的三等奖奖金数；一个一等奖奖金数也和四个单位的三等奖奖金数目相同。

　　因此，每个三等奖奖金数目为：

　　1078÷（4＋4＋3）＝98（元）。

　　一等奖的奖金是：98×4＝392（元）。

　　列出综合算式：1078÷（4＋4＋3）×4＝392（元）。

　　已知△、○、是三个不同的数，并且：

　　△＋△＋△＝○＋○

　　○＋○＋○＋○＝□＋□＋□

　　△＋○＋○＋□＝60，

　　那么△＋○＋□等于多少？

　　答案：45。

　　解析：根据等式一、二可知

　　（○＋○）＋（○＋○＋○＋○）＝（△＋△＋△）＋（□＋□）等式变形后有：6倍的○＝3倍的（△＋□）。

　　从而有2倍的○＝△＋□，

　　由第三个等式得

　　△＋○＋○＋□＝○＋○＋○＋○＝60。

　　可求得○＝15，

　　所以有△＋○＋□＝60-○＝60-15＝45。

是三个不同的数，并且：

　　△＋△＋△＝○＋○

　　○＋○＋○＋○＝□＋□＋□

　　△＋○＋○＋□＝60，

　　那么△＋○＋□等于多少？

　　答案：45。

　　解析：根据等式一、二可知

　　（○＋○）＋（○＋○＋○＋○）＝（△＋△＋△）＋（□＋□）等式变形后有：6倍的○＝3倍的（△＋□）。

　　从而有2倍的○＝△＋□，

　　由第三个等式得

　　△＋○＋○＋□＝○＋○＋○＋○＝60。

　　可求得○＝15，

　　所以有△＋○＋□＝60-○＝60-15＝45。

是三个不同的数，并且：

　　△＋△＋△＝○＋○

　　○＋○＋○＋○＝□＋□＋□

　　△＋○＋○＋□＝60，

　　那么△＋○＋□等于多少？

　　答案：45。

　　解析：根据等式一、二可知

　　（○＋○）＋（○＋○＋○＋○）＝（△＋△＋△）＋（□＋□）等式变形后有：6倍的○＝3倍的（△＋□）。

　　从而有2倍的○＝△＋□，

　　由第三个等式得

　　△＋○＋○＋□＝○＋○＋○＋○＝60。

　　可求得○＝15，

　　所以有△＋○＋□＝60-○＝60-15＝45。