1、成都市“太极杯”象棋比赛，有5 进入到复赛阶段，依据比赛规则进入复赛的5人，每两人要赛一场，胜者得2分，平局者得1分，负者得0分，比赛结果是第一名两人并列，第四名两人并列，请问同学们第三名得_____分。

　　解析：这5个人两两相赛，共需要赛10场，每场有2分，10场共计有20分。

　　每人都要赛4场，即使全部胜了，最多也是8分；但因为有两个第一，所以，第一名不可能是8分，最多是7分。

　　当第一名是7分时，三名不可能是6分，因为第三名不可能胜三场或胜2平2；

　　而第三名是5分也不可能，因为这样一来，两个第4名也不能并列；

　　所以，当第一名得7分时，第三名一定是4分；

　　当第一名得6分时，第三名只能比6分低，5分、2分也不可能，因为剩下的分两个第四名又没法平分了，只能是4分了。

　　当第一名得5分时，第三名只能比5分低，除了4分之外，也没有别的选择了。只能是4分。

　　所以，无论如何，第三名一定得4分。

　　2、如图，找出图形中数字规律，请问第10行第一列数是______。

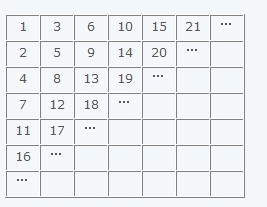
　　解析：第一列数的规律很明显：

　　1、2、4、7、11、16、22、29、37、46

　　3、东方卫视娱乐档邀请五位嘉宾做游戏，每轮游戏都按照箭头的方向把原来手里的毛毛熊或丁丁猪传给另一个人。A→C、B→E、C→A、D→B、E→D，开始时，A、B拿毛毛熊，C、D、E拿丁丁猪，请问传递完5次时拿丁丁猪的嘉宾是 ___、___、___。
　　解析：通过观察我们可以发现，在这五个人中，A和C是一个小团体，不和别人发生联系；那么经过5次传递，最后丁丁猪又回到了C的手中。

　　我们再看B手里的毛毛熊，经过5次传递，B→E→D→B→E→D，毛毛熊落在了D的手中，那么那两个丁丁猪自然是有B和E的手中。

　　4、信都小学每年12月30日都要举办“迎新年”长跑活动，今年长跑路线是绕学校一圈，全长3000米，长跑活动当天学校在跑步沿线每隔60米安排一名家长志愿者，每两名家长之间安排一名学校老师维持秩序，请问信都小学“迎新年”长跑活动中跑步没线安排老师_____人。

　　解析：一圈全长是3000米，如果从起跑点开始每隔60为一个点，那么一圈下来共有3000/60=50个点。起点和终点是同一个点，这个点有校长把着，不需要家长志愿者，那么还有59个点，每个点一名家长志愿者，共需要59人；这59个之间形成了58个间隔，每个间隔安排1名老师，所以需要58名老师。

　　5、刘莉把50枚黑色围棋子排列在五边形的五条边上，每条边上的黑棋子个数相等，且每个角上各有一枚。然后在怕有相邻的两枚黑棋子间放两枚白棋子，请问：这个五边形上共有黑白棋子共_____枚。

　　解析：这五十枚黑色围棋子围成了一个封闭的五边形，所以有50个间隔，每个间隔放两枚白色围棋子，50×2=100(枚），再加上原有的50枚黑色围棋子，共有100+50=150（枚）

　　6、如下图，有一个正方形以它的一条对角线为边做新正方形，又以新正方形的对角线为边做新的正方形；如此做下去行到第四个正方形的面积是64平方厘米，请问原正方形的面积是_____。

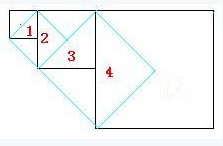
　　解析：通过观察也可以看出，新生成的正方形面积是上一级正方形2倍，所以，原正方形的面积为：

　　64÷2÷2÷2÷2=4（平方厘米）