1、原题：由A、B、C三个班各出3名学生比赛长跑，规定第一名得9分，以后每个名次依次得8，7，6，5，4，3，2，1分。比赛结束后，统计结果时发现三个班总分相等，且没有并列名次，也没有同一班学生得相连的名次，如果第一名是C班的，第二是B班的，那么最后一名是_____班的。

　　解析：三个班的总分是9+8+7+6+5+4+3+2+1=45

　　每个班的得分则是45/3=15。

　　经试算可得：

　　A班成绩：9、2、4

　　B班成绩：8、6、1

　　C班成绩：7、5、3

　　所以，最后一名是B班的。

　　2、原题：在一块展板上，整齐地贴着许多资料，这些卡片的大小相同，卡片之间露出了三块正方形的底色（红），已知资料卡片的短边长度是12厘米，想要配三张图片来把红色部分盖住，需要配的图片的边长是______厘米。

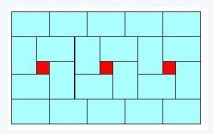
　　解析：这道题主要考察学生的观察能力。

　　通过观察我们发现，卡片的5个长边=3个长边+3个宽边。

　　所以2个长边=3个宽边

　　长边=3*12/2=18

　　长边-宽边=18-12=6（厘米）

　　3、原题：下图是一个长方形的草坪，中间有两个人行道，则草坪的面积是______平方米。

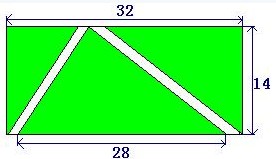
　　解析：最简单的方法是：28*14=392（平方米）

　　稍复杂一点方法是：32*14=448

　　(32-28)/2=2

　　2*2*14=56

　　448-56=392（平方米）

　　4、原题：现在砝码质量为1克、2克、4克、8克、16克、32克的各一枚，在天平上能直接称出_____种不同的质量。

　　解析：这可以看成是一道二进制问题。

　　这六个砝码在天平能称出的最大重量是32+16+8+4+2+1=63（克）

　　这六个砝码能，而且只能称出63克以下的所有整克数质量，

　　所以说能称出63种不同的质量。