原题1：图中一共有（）个长方形（不包含正方形）。

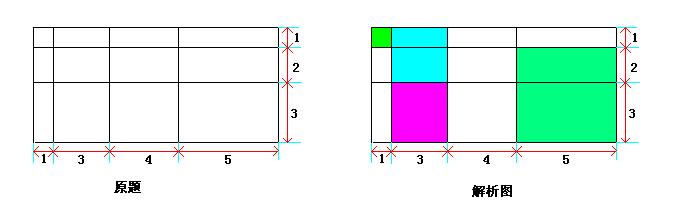
　　解析：数图形问题。

　　如果正方形算是特殊的长方形的话，那么图中共有长方形为：10*6=60（个）

　　由于题中特别注明不包含正方形，所以需要减去图中的几个正方形。

　　如解析图，共有4个正方形，所以，长方形个数为60-4=56（个）

　　这道其实也是一道陷阱题，因为稍不留神，就会把3*（1+2）那个正方给忽略掉。

　　原题2：

　　解析：空间几何问题，这样题在决赛中还会出现。本题所对应的培训题是第47题。

　　用投影（照射）法来进行计算。

　　从前后两面看，能看到的平面是2*11个

　　从左右两侧看，能看到的平面是2*8个，

　　从上下两面看，能看到的平面是2*11个，

　　共有：60个平面，每个平面的面积是1平方厘米，共有60平方厘米。

　　原题3：手工课上，小红用一张直径是20厘米的圆形纸片剪出如图所示的风车图案，则被剪掉的纸片（阴影部分“的面积是（）平方厘米。

　　解析：这是一道平面几何计算，用排除法来求解。

　　先求出整个图形的面积，

　　再求出四个小半圆的面积，两者相减，即得解。

　　原题4：买72块巧克力共花了□67.9□元，求每块巧克力多少元？

　　解析：这是一道标准的整除问题，学过整除计算的同学都能做出来。对应的题是第28题。基本和原题是一样的，只是换了个数字而已。

　　既然能被72整除，那么就一定能被8和9整除。

　　根据能被8整除的特点，可知后面一个方框里的数是2，

　　又因为能被9整除，各个数位之和一定是9的倍数，6+7+9+2=24   27-24=3

　　所以，这72块巧克力的价钱是367.92元，则每块巧克力的价钱是：5.11元。

　　原题5：两个自然数的最小公倍数是140，最大公约数是5，则这两个数的和的最大值是 （）。

　　解析：约数倍数问题，和第29题对应。

　　要想让这两个数的和最大，那就要让两个数尽量离的开些。

　　小的数，最小可以两数的最大公约数；大的数，最大可以是两数的最小公倍数。

　　所以：5+140=145

　　原题6：一条项链上共串有99颗珠子，如图。其中第一颗珠子是白色的，第2、3颗珠子是红色的，第4颗珠子是白色的，第5、6、7、8颗珠子是红色的，第9颗珠子是白色的，……则这条项链中共有红色的珠子（）颗。

　　解析：周期性问题加等差数列求和。

　　把该项链分成若干组，每组的第一个为白色，则每组有珠子数为：

　　3、5、7、9、11、13、15、17、19，

　　99颗珠子刚好可以分成9组，每组有一个白色的珠子，9组有9个白色珠子，所以红色珠子数为：

　　99-9=90（颗）

　　原题7：在循环小数0.123456789中，将表示循环节的圆点移动到新的位置，使新的循环小数的小数点后第2011位上的数字是6，则新的循环小数是（）。

　　解析：第2011位上的数字是6，则第2012位上的数字是7，第2013位上的数字是8，2014位上的数字是9。

　　从第10位数字开始，到第2014位，是整数个循环节。

　　2014-9=2005  2005=5*401   所以，每个循环节有5个数字，所以，表示循环的点在5和9上面。

　　说明：第1、2、3、4题比较简单，绝大多数同学都做对了，加之上传图片较烦琐，故在此略去。

　　只公布一下答案：

　　1、五又三分之二

　　2、七分之十八。

　　3、5.4   一又165分之23