原题1：196名学生按编号从1到196顺次排成一列。令奇数号位（1、3、5、…）上的同学离队，余下的同学顺序不变，重新自1从小到大编号，再令新编号中奇数位上的同学离队，依次重复上面的做法，最后留下一位同学。这位同学开始的编号是（）号。

　　解析：这是一道典型的抽杀问题，简单到三年级的同学也能直接把答案写出来，当然这要有个前提条件，就是见过这类题。

　　这道题对应的是培训题的最后一道题，当然它的份量太轻了，所以前面的第13题和它结伴出现。

　　以我的想法。即使是这样，培训题中的第100题仍然是意犹未尽，很可能在决赛中再次出现，能否言中，一个月后见。

　　为了帮助从未见过这题的同学理解，在这里我就多讲几句。

　　第一轮下来，剩下的同学原编号是：2、4、6、8、10、12、……，它们都是2的倍数；

　　第二轮下来，剩下的同学原编号是：4、8、12、16、20、24、…… ，它们都是4的倍数。

　　第三轮下来，剩下的同学原编号是：8、16、24、32、40、48、……，它们都是8的倍数

　　第四轮下来，剩下的同学原编号是：16、32、48、64、80、……，它们都是16的倍数

　　第五轮下来，剩下的同学原编号是：32、64、96、128、160、192，     它们都是32的倍数。

　　第六轮下来，剩下的同学原编号是：64、128，只剩下这可怜的难兄难弟了，它们都是64的倍数。

　　最后一轮下来，就只剩下独孤求败的128号了。

　　原题2：人口普查员站在王阿姨家门前问王阿姨：“您的年龄是40岁，您收养的三个孤儿的年龄各是多少岁？”王阿姨说：“他们年龄的乘积等于我的年龄，他们年龄的和等于我家的门牌号。”普查员看了看门牌号，说：“我还是不能确定他们的年龄。”，那么，王阿姨家的门牌号是（）。

　　解析：这道题是一个年龄与约数的问题。仍然和第15、31、25题有对应关系。

　　40=1*1*40（）  1+1+40=42

　　=1*2*20（）  1+2+20=23

　　=1*4*10（）  1+4+10=15

　　=1*5*8（）   1+5+8=14

　　=2*2*10（）  2+2+10=14

　　=2*4*5（）   2+4+5=11

　　王阿姨家的门牌号普查员是知道的，但还是不能确定几个孩子的年龄，说明什么问题，说明这几个孩子的年龄和两种情况，都等于门牌号，所以，此题的答案是14。

　　原题3：沿着圆周放置黑、白棋子各100枚，并且各自相邻排列，若将圆周上任意两枚棋子换位一次称为一次对换，则最少经过（）次对换可使全部的黑棋子彼此不相邻。

　　解析：这是一道操作类问题。对应培训题的第96题。

　　解操作类问题，关键是要找到内在规律，问题就好办了。

　　先把顶端相邻的黑白棋子编号为黑1和白1，之后往分别往两边依次编号为：黑2、黑3、黑4……；白2、白3、白4……，黑1的白1对换，下一对黑3与白3对换，再往后，黑5与白5对换，…到最后，黑99与白99对换，共50次。

　　原题4：图中每个圆圈内的汉字代表1--9中的一个数字，汉字不同，数字也不同，每个小三形三个顶点上的数字之和相等。若7个数字之等于12，则“杯”所代表的数字是（）。

　　解析：这是一道数阵图题，虽然培训题没有给出，但作为六年级的学生来讲，完全能够也应该掌握。

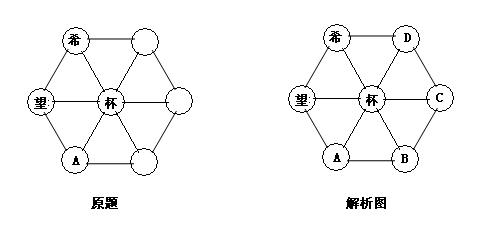
　　因为每个小三角形三个顶点上的数字之和都相等，

　　所以：   希+望+杯=望+杯+A=杯+A+B=杯+B+C=杯+C+D

　　所以：希=A=C   望=B=D

　　所以。希+希+希+望+望+望+杯=12

　　进一步可知，杯=3。