2013年第十一届"小机灵杯"数学竞赛决赛四年级试题

1、暂缺

2、110除以一个两位数的余数是5，符合条件的所有两位数是______。

3、把2012写成N个互不相同的正整数的和，N最大等于______.

4、1×1+2×2+3×3+…2011×2011+2012×2012的之和最后一位数字是______.

5、暂缺

6、把一个三位数的百位与个位上的两个数字交换，十位数字不变，所得的新数与原数相等，这样的数共有______个，其中能被4整除的有_____个。

7、暂缺

8、将编号是1、2、3、…15的十五名学生按编号顺序面向里站成一圈，第一次，编号是1的同学向后转，编号是2、3、的同学向后转，第三次编号是4、5、6的同学向后转，….第15次，全体同学向后转，当转完第12次时，这时面向外的同学还有______名。

9、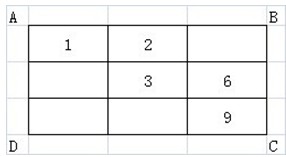

求长方形ABCD的面积是多少？

10、暂缺

11、把1到200这两百个自然数中，既不是3的倍数，又不是5的倍数的数从小到大排成一排，其中第100个数是_______.

12、黑板上一共写了165个数，包括11个11，,12个12,13个13,14个14,15个15，每次操作都擦去其中4个不同的数并写上一个第5种数（如擦去11、12、13、14，写上一个15，或者擦去12、13、14、15，写上一个11…），如果经过若干次操作后，黑板上恰好剩下了2个数，那么，这两个数是______、_____。

13、还有一道大题目，孩子来不及抄出来，大致上讲了一下，是体育比赛的，

14、暂缺

15、问得是所有三位回文数之和是多少？