一、初赛试卷总结

　　华杯初赛已经过去几天，不管孩子考试怎么样，分高或者分低都已经不重要，重要的是赶紧查漏补缺，把不会做的和做错的题都学会，下次考试把这些没拿到的分拿到手才最重要。下面是笔者对每道题考点的分析以及与课本内容的联系。

　　综合来看，今年的考点仍然和课本内容联系密切，这意味着孩子在复习时还是应该回归课程，把前面的已学的内容吃透、再吃透。

　　试题难度上除了三道三星题以外，大部分都是二星的题目，绝对算不上难；与去年初赛对比，今年初赛的难度降低了不止一个档次。因此，去年华杯赛晋级的分数线是五年级50分，六年级60分，预计今年的晋级分数线为五年级60或70分，六年级70分。

　　二、决赛考点预测

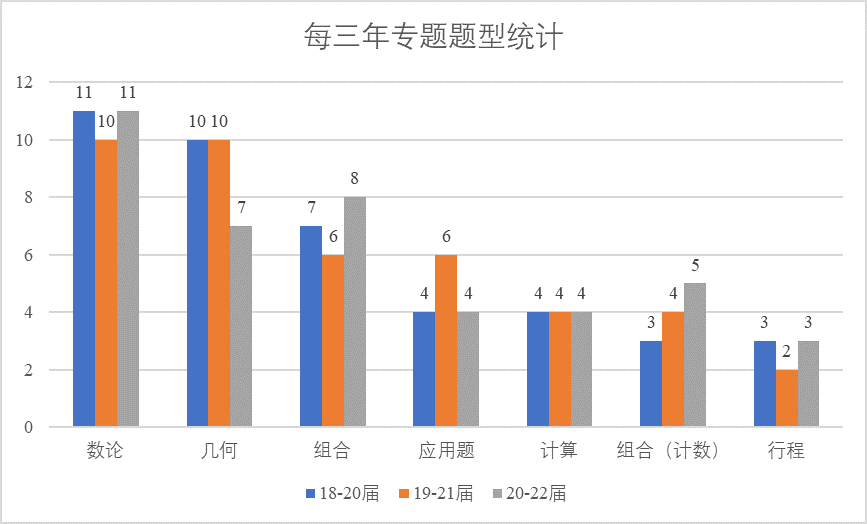
　　从整体而言，试卷结构比较固定，以数论和几何为主要考点，然后是组合，其余如应用题、行程和计数类组合题平均每次1题。但如果以单卷而言，试卷结构就有些夸张了，近三年试卷考点标注如下：

　　可以发现，上一届的组合部分（包括计数在内）的占比极高，而数论相较变少，不过计算和行程以及几何仍然保持至少1题的状态，所以在准备时，准备的重点仍然是组合+数论，这一点是不会改变的。

　　对近五年的知识点分析：

　　组合部分几乎清一色的构造题，其中和数字有关的构造总计超过7个，所以说毫无疑问是考试必备考点之一，和数字构造有关的题目主要和数字和特性以及数字谜有关；而图形构造则以构造染色的居多。所以组合部分可以着重练习构造类题目。

　　然后就是组合（计数）最具特点，因为几乎都是枚举，6个，就一个考点已经是一个很夸张的数字了，足以说明这个知识点是有多么的被重视，其实这也是一个必然的状况，只要不是太过死板的数学题目，一定会存在灵活解题思路和方向，而往往这种偏开放性的题目就极易使用到枚举，包括上面的构造，在提笔的开始时也是从枚举中寻求解题思路的，所以学习枚举，使用枚举，高效枚举，是学习数学极需求的技能之一，也是杯赛中经常考察的关键点之一！

　　再说数论，数论题目主要分余数类和因数类。余数类出现三次剩余问题，两次同余问题，余数问题虽然形式各异，但拨开表面以后，剩余的部分完全没有任何变化，换句话说，只要能发现是余数问题，那么就是固定做法，所以是比较容易准备的题目，必备。而因数类则主要以带字母的两数要互质或不能互质作为考点，所以要注意整除特征，质因数分解和辗转相除（减）三个知识点。

　　其余如应用题，基本以分数应用题为主，有时为工程问题或浓度问题；若出现一般应用题，则可能考察平均数问题和周期问题，因为这两点可以作为统计基础，而且其他一般应用题则多可用方程极易解决，参考性差，所以几何没有出现过。虽然上一届并没有出现应用题，但一直以来都是1-2个左右，所以也可稍作准备，以分数三大应用题为主，平均数问题和周期问题为辅。

　　几何题主要考察两部分，一部分是课内例如平面曲线图形的计算，以及长方体类型题的计算，另一部分则是模型的考察，所以在准备几何时，课内内容一定要抓好，再另做比例模型的准备，优先准备风筝模型，题型覆盖更广。

　　行程题出现次数少，所以很难预测，不过更偏向准备比例行程题，例如多人相遇问题和环形多次相遇问题可能性也许更高！

　　计算题就没有什么好总结的了，固定第一题一定和计算有关，而且只要不犯粗心，一般没什么大问题，如果想准备难点的话，可以熟练裂项的使用。