10、把123，124，125三个数分别写在图10-2所示的A，B，C三个小圆圈中，然后按下面的规则修改这三个数。第一步，把B中的数改成A中的数与B中的数之和;第二步，把C中的数改成B中(已改过)的数与C中的数之和;第三步，把A中的数改成C中(已改过)的数与A中的数之和;再回到第一步，循环做下去。如果在某一步做完之后，A，B，C中的数都变成了奇数，则停止运算。为了尽可能多运算几步，那么124应填在哪个圆圈中?

　　11、若干个同样的盒子排成一排，小明把五十多个同样的棋子分装在盒中，其中只有一个盒子没有装棋子，然后他外出了。小光从每个有棋子的盒子里各拿一个棋子放在空盒内，再把盒子重新排了一下。小明回来仔细查看了一番，没有发现有人动过这些盒子和棋子。问共有多少个盒子?

　　解答：原来有个空的，说明现在也有个空的;现在空的说明原来这盒有1个，当然现在也必须有个盒子有1个;现在盒中有1个，说明原来是2个，当然现在也必须有个盒子有2个;……考虑50多，所以有0+1+2+3+4+5+6+7+8+9+10=55共11个盒子。

　　12、如图10-3，圆周上顺序排列着1，2，3，……，12这12个数。我们规定：把圆周上某相邻4个数的顺序颠倒过来，称为一次变换，例如1，2，3，4可变为4，3，2，1，而11，12，1，2可变为2，1，12，11。问能否经过有限变换，将12个数的顺序变为如图10-4所示的9，1，2，3，……，8，10，11，12?

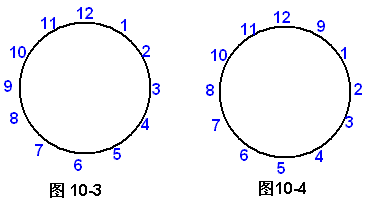
　　解答：从两个图可以看出，10、11、12没有变化，我们不妨这样排列：9、8、7、6、5、4、3、2、1变为8、7、6、5、4、3、2、1、9;这样只要9次就行。

　　13、在一块黑板上将123456789重复50次得到450位数123456789123456789……。先删去这个数中从左至右数所有位于奇数位上的数字，再删去所得的数中所有位于奇数位上的数字，……，依此类推。那么，最后删去的是哪个数字?

　　解答：容易发现，每次留下的应该是2^n位上的数字;2^8=256，2^9=512>450，所以最后一个数字应该是第256位上的数;256/9=28......4，所以，最后删去的是4。

　　14、把1，2，3，4，……，1986，1987这1987个数均匀排成一个大圆圈，从1开始数：隔过1划掉2，3，隔过4划掉5，6，这样每隔一个数划掉两个数，转圈划下去，……。问：最后剩下哪个数?

　　15、如图10-5，在一个圆周上放了1枚黑色的和1990枚白色的围棋子。一个同学进行这样的操作：从黑子开始，按顺时针方向，每隔1枚，取走1枚。当他取到黑子时，圆周上还剩下多少枚白子?

　　解答：将黑子右边的第一个编号1，顺时针排下去，到黑子就是第1991号;每隔1枚，取走1枚，即第一圈取所有偶数编号的，最后一颗取走的为1990号，即黑子左边的一个，到黑子时正好跳过黑子;这样第一圈共取走(1991-1)/2=995个，留下了996个;对剩下的棋子重新按上述方法(即黑子右边为1号)编号，第2圈就变成了全部取走奇数号，因为此时黑子为996号，又正好留下;并且可以知道，只要留下的是偶数枚，黑子总能跳过;992/2=498，第三圈留下498枚;498/2=249，第四圈留下249枚;249为奇数，因此第5圈结束将正好取走黑子，那么，当黑子被取走时，还留下(249-1)/2=124枚。

编辑推荐:

第十七届华杯赛笔试考试注意事项

华杯赛知识点模块考点分析汇总

2012华杯赛备考分三个阶段进行