第九届小学“希望杯”全国数学邀请赛六年级二试
第九届小学“希望杯”全国数学邀请赛六年级二试








点击下一页查看答案
1. 原式=3.625+0.(45)-1.(36)=2.625+(1.(45)-1.(36))=2.625+0.(09)
=2.715(90)。(这里用括号代替表示循环节)
2. 后一部分等于(4×1.5)÷(4+1.5÷3)=4/3,而0.(36)=4/11,
所以原式=(2×4/11+4/3)÷(4/11+2×4/3)=(2/11+1/3)÷(1/11+2/3)
=17/25。
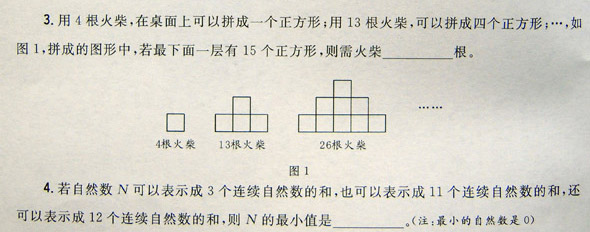
3. 第二个图形比第一个图形多9根火柴,第三个图形比第二个图形多13根火柴,
经尝试,第四个图形比第三个图形多17根火柴,而最下面一层有15根火柴
的是第8个图形,所以共需要火柴4+(9+13+17+21+25+29+33)=151根。
4. 因为奇数个连续自然数之和等于中间数乘以数的个数,所以N能被3和11
整除,也就是能被33整除;
因为偶数个连续自然数之和等于中间两个数的平均值乘以数的个数,所以
N等于一个整数加上1/2再乘以12,也就是被12除余6,最小为66。
66可以表示成0到11的和。
5. 4m+5=5n+4,也就是说4(m-1)=5(n-1),如果m-1=5,n-1=4,则m=6,n=5,
但此时n进制中不能出现数字5;如果m-1=10,n-1=8,则m=11,n=9,
符合题意。
6. 1949+60=2009,而2009年是己丑年,所以1949年是己丑年。
7. 每次摸出的结果可能是两个球颜色相同,有3种可能;或颜色不同,也有
3种可能,共6种可能。最不利情况是每种可能各出现4次,则再摸一次就
保证有5次相同,6×4+1=25。
8. 相当于分别从1和1002处以2:5的速度比进行相遇问题,
(1002-1)÷7×2+1=287。
9. 连接两个正方形的"\"的对角线,发现它们平行,所以阴影部分的面积
就等于一个扇形的面积,为15×15×3÷4=675/4。
10. 总共价格为n^2元,最后乙付说明n^2的十位数字为奇数,所以个位为6,
乙最后一次付了6元,应该给甲2元。
11. 前5位队员的平均身高比前8位队员的平均身高多3厘米,也就是说,加入
第6~8名后,平均身高减少了3厘米,因此第6~8名的平均身高比前5名的
平均身高少3÷3×8=8厘米。
第9~23位队员的平均身高比第6~23位队员的平均身高少0.5厘米,也就是说,
加入第6~8名后,平均身高增加了0.5厘米,因此第6~8名的平均身高比第9~23名的
平均身高多0.5÷3×18=3厘米。
因此,前8名的平均身高比第9~23名的平均身高多8-3+3=8厘米。
12. 根据对称性,丙先带谁没有区别。设先带甲,返回接乙。
设乙步行的路程为x,丙骑车返回的路程为y,甲步行的路程为z。
乙比骑车从A地到B地多用时间x(1/5-1/12),甲比骑车从A地到B地多用时间
z(1/4-1/12),丙比骑车从A地到B地多用时间2y/12。
这三个相等时,x:y:z=10:7:7,所求路程比为7:10。
13. 车速提高20%,也就是变成原来的6/5,则时间变成原来的5/6,
减少25分钟,原定时间为25×6=150分钟;
车速提高25%,也就是变成原来的5/4,则时间变成原来的4/5,
减少10分钟,则这段路程的原定时间为10÷5=50分钟。
因此,原速行驶100千米需要150-50=100分钟,
距离为150÷100×100=150千米。
14. 两次的空白部分体积相等,而第二次的空白部分的横截面积为第一次的
1-1/8=7/8,所以第一次的空白部分的高度为第二次的7/8,即7厘米。
正方体的底面积为20×20=400平方厘米,所以圆柱体的底面积为400÷8=
50平方厘米,高度为20-7=13厘米,体积为50×13=650立方厘米。
15. 全胜的队得7分,而最后四队之间赛6场至少共得6分,所以第二名
的队得分至少为6分。如果第一名全胜,则第二名只输给第一名,得6分;
如果第二名得6.5分,则第二名6胜1负,第一名最好也只能是6胜1负,
与题目中得分互不相同不符。所以,第二名得分为6分。
16. (45,80)→(45,35)→(10,35)→(10,25)→(10,15)→(10,5)→(5,5)。
这就是用辗转相除法求最大公约数的运算,所以两个四位数的最大公约数
为17,9999÷17=588……3,所以最大的四位数是9999-3=9996,第二大的
四位数是9996-17=9979,和为19975。









