备战华杯赛,试题每日一练(16)
杭州奥数网2月1日 进入2013年,第十八届“华杯赛”的考试也将近,备战华杯赛刻不容缓,即日起,每天整理1-3道华杯赛试题,给备考的学生们练手准备,继续每日一练(16)。更多信息请点击>>
试题一:
一组互不相同的自然数,其中最小的数是1,最大的数是25,除1以外,这组数中的任一个数或者等于这组数中某一个数的2倍,或者等于这组数中某两个数之和。问:这组数之和最大值是多少?当这组数之和有最小值时,这组数都有哪些数?并说明和是最小值的理由。
答案:这样一组数的和的最大值是325;最小值存在,是61。
分析与解:(1)考虑数组中各数和最大的情形
显然,最大的数组是1到25的全部都取,它的确满足要求。所以,这组数之和最大值是
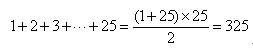
(2)考虑数组中各数和最小的情形
这数组中肯定有1,也必有2,不然就没有别的数了。根据“这组数中的任一个数或者等于这组数中某一个数的2倍,或者等于这组数中某两个数之和”,把它们按从小到大的顺序排列起来,排到第四个数,可能出现的情况只有以下6种:
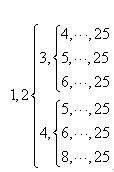
最后一个数25是偶数,它只能是比它小的另外两个不同数之和。在这6种可能性中,虚线表示的没有写出来的数里面,至少要有两个数,它们的和不小于25,不然的话,最后的25就表不成组中某两个数之和。为使数组中各数之和尽量小,应当在“…”填尽量少的数,并使填入的数之和尽量小。
在1,2,3,4,…,25中,“…”处可以只填10,15两个数,就使两个数之和25,并且满足对数组的各项要求。因为,在以后的其他情形里,即便能够只填入两个数,它的各数之和也都变大了;而填入三个数的话,后两个数之和为25,整个和就更大了。所以,数组1,2,3,5,10,15,25的和是最小的,这个最小的和等于
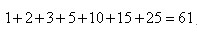
答:这样一组数的和的最大值是325;最小值存在,是61。
试题二:
设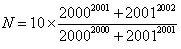 ,求N的整数部分。
,求N的整数部分。
答案:20009
解: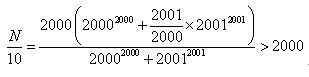
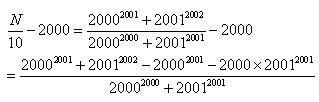

而
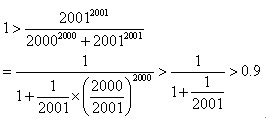
所以 
N的整数部分是20009。
来源:华杯赛官网
>>推荐阅读








