备战华杯赛，试题每日一练(12)
杭州奥数网1月28日 进入2013年，第十八届“华杯赛”的考试也将近，备战华杯赛刻不容缓，即日起，每天整理1-3道华杯赛试题，给备考的学生们练手准备，继续每日一练(12)。更多信息请点击>>
试题一：
师徒二人加工规定了数量的一批零件，按加工零件数目的比例分配3000元的报酬。如果按原计划进行的速度，师傅应该得到1800元，但是结果师傅每天比计划多加工了10个零件，于是实际得到了2040元，那么徒弟每天加工多少个零件？
分析：解决本题首先需要理解报酬的分配方法，也就是当师徒二人完成任务后，该如何分配这固定的3000元报酬呢？根据已知（也符合实际生活），报酬分配的比例就是两人加工零件数目的比例，也就是个人工作总量的比例。那么由于两个人的工作时间是相同的，此时工作总量与工作效率成正比，所以报酬分配的比例也就是两人工作效率的比例。
解：师徒原先的工作效率比是：1800﹕（3000-1800）＝3﹕2 。
后来师徒二人的工作效率比是：2040﹕（3000-960）＝17﹕8。
徒弟每天加工的零件数：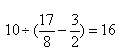
（个）。
答：徒弟每天加工16个零件。
说明：由于一般几个人合作时，他们的工作时间相同，所以报酬分配的比例就等于工作效率的比例，因此题目条件中如果出现了报酬金额，就可以转化为工作效率的比例条件。而如果工作时间不同，那么报酬分配的比例就不一定等于工作效率的比例了，只能计算工作总量的比例。
试题二：
某校组织148名同学到外地实习，出发这天早晨，他们在5﹕30集中从学校出发，必须在7﹕25赶到火车站。临时只有一辆可乘50人的大客车送他们走。车速在36千米/小时，学校离火车站21千米。如果所有同学都用车送，大客车得往返多次，时间来不及。因此只有乘车与步行穿插进行。假定同学步行的速度是4千米/小时 ，那么有没有办法能保证他们准时到达火车站？（不计上下车时间）。
分析与解：148人至少要分三批乘车。最好（快）的方法是：第一批同学乘车，第二、三批同学步行同时从学校A出发去火车站B,当到途中某地E时，第一批学生下车改步行，大客车返回，在C处接上第二批同学前往火车站，到某处F时让他们下车改步行，大客车返回，在D处接上第三批同学直接开到火车站B，而且三批同学恰好同时到达。如图所示：
不妨假定三批同学的乘车时间相同，步行的时间也相同，图中1，2，3分别表示三批同学步行的情况。
由对称性知，AC=CD=EF=FB.
设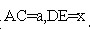
。由上图知每批学生步行的路程为2a，大客车在第三批同学步行的时间里行使了
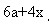。因为大客车的速度是步行速度的9倍，得
。
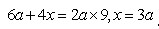由AB=7a=21（千米） a=3（千米）。
每批同学都步行6千米，乘车15千米，可同时到达火车站。所用时间为
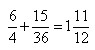（小时）＝1小时55分。
答：他们在5﹕30出发，可以7﹕25赶到火车站。
来源：华杯赛官网
>>推荐阅读
