2011年第九届“希望杯”五年级第2试答案详解
希望杯的获奖比例比较大,孩子如果能够拿到一个奖项,对于孩子以后的学习兴趣和学习热情的激发都是具有非常重要的导向作用,下面是2011年第九届“希望杯”五年级第2试答案。查看试题:2011年第八届“希望杯”五年级第2试试题。
1. 原式=0.15×56÷2.1=8.4÷2.1=4。
2. 原式=(11+111+1111+...+1111111111)+4×9=1234567899+36=1234567935。
3. 所得的商除以4,余数为3,设此商为4a+3,则原数为3(4a+3)+2=12a+11,
除以6,商2a+1,余数为5。
4. 1×1的有10个;
1×2和2×1的各有6个;
1×3和3×1的各有3个;
1×4和4×1的各有1个;
2×2的有3个;
2×3和3×2的各有1个;
共有10+6+6+3+3+1+1+3+1+1=35个。
5. 既是完全平方数又是完全立方数的数一定是完全六次方数,1^6=1,
2^6=64,3^6=729,4^6=4096超过1000,所以共有3个。
6. 最小的一个约数是1,所以第二小的约数是5。最大的约数是它本身,所以第二大的约数是它的五分之一,差是原数的五分之四,所以原数等于308÷4×5=385。
7. 经试验:黑黑黑黑白→白白白黑黑→白白黑白黑→白黑黑黑黑,出现了循环,
所以最多有3个白子。
8. 设甲每分钟走的路程为3,乙每分钟走的路程为1,则前60分钟甲走了180,乙走了60。甲的速度减为原来的一半,即1.5,甲走到B地还有60的路程,需要时间为60÷1.5=40,乙走到A地还有180的路程,需要时间为180÷1=180,所以需要时间为180-40=140。
9. 每锯一次增加2个面的表面积,锯了6次共增加12个面的表面积,加上原来的6个面,共有18个面的表面积,为18。
10. 两次倒之后,桶的空出部分是不变的,所以小丽的桶的容积的一半等于小明的桶的容积的1/4,也就是说小明的桶的容积等于小丽的桶的2倍。小丽的桶的容积的一半加上小明的桶的容积等于8千克,也就是说,小明的桶的容积的1/4加上小明的桶的容积等于8千克,小明的桶的容积等于
8÷(5/4)=6.4千克,小丽的桶的容积等于6.4÷2=3.2千克。
11. 每四个括号一个周期,相邻的两个周期的对应数之差为16。
2011以内,16的倍数中最大的是2000,所以最后一组括号应该是(2001),(2003,2005),(2007,2009,2011),最后一个括号的三个数之和为6027。
12. 设小明1岁时,爸爸x岁,爷爷2x岁,则爷爷61岁时,爸爸为
x+61-2x=61-x岁,小明为1+61-2x=62-2x岁,所以61-x=8(62-2x),
得到x=29。也就是说,小明1岁时,爸爸29岁,爷爷58岁。爷爷比小明大57岁。当爷爷的年龄是小明年龄的20岁时,小明57÷(20-1)=3岁,爸爸31岁。
13. 只要答案合理即可。如图。
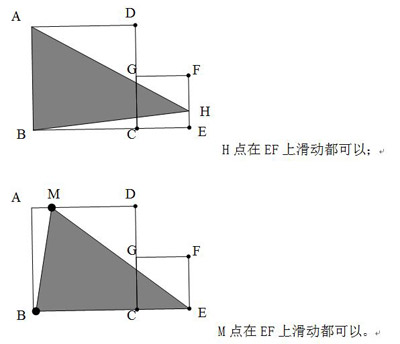
14. 设丁钓到x条鱼,丙钓到y条鱼(x<y),则乙钓到x+y条鱼,甲钓到x+2y条鱼,四个人共钓到3x+4y条鱼。因此,3x+4y=25。因为25被4除余1,所以x被4除余3。
如果x=3,则y=4,x+y=7,x+2y=11;
如果x=7,则y=1,不符合x<y。
因此,甲钓到11条鱼,乙7条,丙4条,丁3条。
15. 第一次相遇时两车共走1个全程,第二次相遇时两车共走3个全程,所以第二次相遇时,甲车共行驶180千米。
第二次相遇点可能距离甲地80千米或40千米,也就是说180千米比全程的2倍少80千米或40千米,两地距离为130千米或110千米。
130-60=70,110-60=50,所以乙车的速度是70千米/时或50千米/时。
16. 2011×2被9除的余数等于(2+0+1+1)×2被9除的余数,即8。
N被9除的余数等于7n被9除的余数,它等于7×3被9除的余数,即3。
编辑推荐:








