2008“数学解题能力展示”读者评选活动

六年级组初赛试题

（测评时间：2007年12月2日9：00—10：30；满分150）

一、填空题Ⅰ（每题8分，共40分）

1.         计算：［2007-(8.5×8.5-1.5×1.5)÷10］÷160-0.3＝　　　　　　。

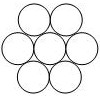
2.         七个同样的圆如右图放置，它有            条对称轴。

3.         大正方体的棱长是小正方体棱长的4倍，那么它的表面积是小正方体表面积的   　　倍。

4.         甲、乙、丙三件商品，甲的价格比乙的价格少20％，甲的价格比丙的价格多20％；那么，乙的价格比丙的价格多              ％。

5.         分别以一个边长为2厘米的等边三角形的三个顶点为圆心，以2厘米为半径画弧，得到右图；那么，阴影图形的周长是    　       厘米。

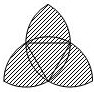  （π取3.14）

二、填空题Ⅱ（每题10分，共50分）

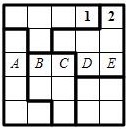
6.         如图，5×5方格被分成了五块；请你在每格中填入1、2、3、4、5中的一个，使得每行、每列、每条对角线的五个数各不相同，且每块上所填数的和都相等。现有两个格子已分别填入1和2，请在其它格子中填上适当的数。那么，ABCDE这个五位数是：           。

7.         已知九位数2007□12□2既是9的倍数，又是11的倍数；那么，这个九位数是：                 。

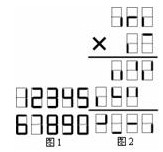
8.         电子数字0～9如图1所示，图2是由电子数字组成的乘法算式，但有一些已经模糊不清。请将图2的电子数字恢复，并将它写成横式：

9.         A、B两地相距22.4千米。有一支游行队伍从A出发，向B匀速前进；当游行队伍队尾离开A时，甲、乙两人分别从A、B两地同时出发。乙向A步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾……当甲第5次追上队头时恰与乙相遇在距B地5.6千米处；当甲第7次追上队头时，甲恰好第一次到达B地，那么此时乙距A地还有　  　千米。

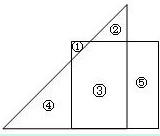
10.         一个等腰直角三角形和一个正方形如图摆放，①、②、③这三块的面积比依次为1:4:41。那么，④、⑤这两块的面积比是　　　　　　。

三、填空题Ⅲ（每题12分，共60分）

11.         有4个不同的数字共可组成18个不同的4位数。将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数。那么这18个数的平均数是：                。

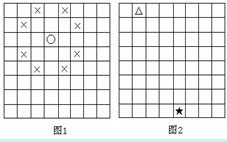
12.         国际象棋中“马”的走法如图1所示，位于○位置的“马”只能走到标有×的格中，类似于中国象棋中的“马走日”。如果“马”在8×8的国际象棋棋盘中位于第一行第二列（图2中标有△的位置），要走到第八行第五列（图2中标有★的位置），最短路线有        条。

13.         将0～9这十个数字分别填入下面算式的□内，每个数字只能用一次；那么满足条件的正确填法共有         种。

□＋□□＋□□□＝□□□□

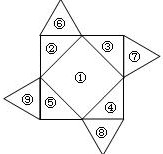
14.         右图是个有底无盖的容器的平面展开图，其中①是边长为18厘米的正方形，②③④⑤是同样大的等腰直角三角形，⑥⑦⑧⑨是同样大的等边三角形。那么，这个容器的容积是              毫升。

15.         有10个整数克的砝码（允许砝码重量相同），将其中一个或几个放在天平的右边，待称的物品放在天平的左边，能称出1，2，3，…，200的所有整数克的物品来；那么，这10个砝码中第二重的砝码最少是　　　　　　克。

［答案］

一、填空题Ⅰ（每题8分，共40分）

1.         12.2

2.         6

3.         16

4.         50

5.         12.56

二、填空题Ⅱ（每题10分，共50分）

6.         14523

7.         200731212

8.         122×25＝3050

9.         14.4

10.     9:14

三、填空题Ⅲ（每题12分，共60分）

11.     6444

12.     12

13.     60

14.     2430

15.     18