2008“数学解题能力展示”读者评选活动四年级组初赛试题
2008“数学解题能力展示”读者评选活动四年级组初赛试题
(测评时间:2007年12月2日11:00—12:00;满分150)
一、填空题Ⅰ(每题10分,共60分)
1. 计算:12345×2345+2468×38275= 123450000 。
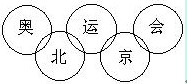
2. 2008年奥运会在北京举行。“奥”、“运”、“会”、“北”、“京”这五个汉字代表五个连续的自然数,将其分别填在五环图案的五个环内,满足= 。这五个自然数的和最大是 30 。
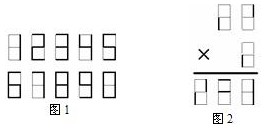
3. 电子数字0~9如图1所示,图2是由电子数字组成的乘法算式,但有一些模糊不清,请将图2的电子数字恢复,并将它写成横式形式: 28×8=224 。
4. 如图,4×4方格被分成了五块。请你在每格中填入1,2,3,4中的一个,使得每行、每列的四个数各不相同,且每块上所填数的和都相等。那么,A、B、C、D处所填的四个数的和是 10 。

5 一个书架上有数学、语文、英语、历史4种书共35本,且每种书的数量互不相同。其中数学书和英语书共有16本,语文书和英语书共有17本。有一种书恰好有9本,这种书是_____英语_____书。
6 袋中有3个红球,4个黄球和5个白球,小明从中任意拿出6个球,他拿出球的情况共有 18 种可能。
二、填空题Ⅱ(每题15分,共90分)
7 小名、小亮两人玩扑克牌,他们手里各有点数为1、2、3、4、5、6、7、8、9、10的纸牌各一张,两人每轮各出一张牌,点数大的为胜,并将两张牌的点数差(大减小),做为获胜一方的分数,另一方不得分。10轮牌出完之后,两人总分之和最大是 50 。
8 有100个棱长为1厘米的正方体木块,表面均为白色,还有25个棱长为1厘米的正方体木块,表面均为蓝色。将这125个正方体木块粘在一起,形成一个大正方体。大正方体的表面为白色的面积至少是 92 平方厘米。
9 某篮球运动员参加了10场比赛,他在第6、7、8、9场比赛中分别得到了23、14、11和20分,他在前9场比赛的平均分比前5场比赛的平均分要高,如果他10场比赛的平均分超过18分,那么他在第10场比赛至少得 29 分。
10 在纸上写着一列自然数1,2,…,98,99。一次操作是指将这列数中最前面的三个数划去,然后把这三个数的和写在数列的最后面。例如第一次操作后得到4,5,…,98,99,6;而第二次操作后得到7,8,…,98,99,6,15。这样不断进行下去,最后将只剩下一个数,最初的99个数连同后面写下的数,纸上出现的所有数的总和是 25128 。
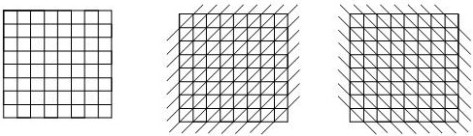
11 在“8×8”的方格中放棋子,每格至多放1枚棋子。若要求8行、8列、30条斜线(如下图所示)上的棋子数均为偶数。那么“8×8”的方格中最多可以放 48 枚棋子。
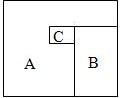
12 如图,一个长方形被分成A、B、C三块,其中B和C都是长方形,A的八条边的边长分别是1、2、3、4、5、6、7、8厘米。那么B和C的面积和最多是 36 平方厘米。(示意图不成比例)