四年级华杯赛备考每日一题(2.16)
距离四年级华杯赛(3月17号)的时间越来越近了,为了让大家更好的备战这一次的四年级华杯赛,永佳老师从今天开始每天都会以每日一题的形式给大家对华杯赛所有可能考到的模块进行一次回顾,希望大家能坚持做题,在华杯赛中获得好成绩!
由于四年级华杯赛是第一年举行,老师会在往年的其他杯赛中选取接近难度的题目,让大家能对四年级华杯赛的难度和考法有更清晰的认识。
规则是这样的,每天早上老师都会更新一道题目,同学们有做出来的就直接回帖把答案和过程放上来,答对的会有金币奖励!老师会在第二天放出上一天的答案详解。另外对于觉得一道题太少的同学,老师还会附上几道拓展的题目,做出来的同学同样可以回帖,答案同样会在第二天放出。
今天的题目还是关于平面几何,今天的专题是公式法求面积。公式法是面积求解中比较难的方法,大家要加强重视呀!~
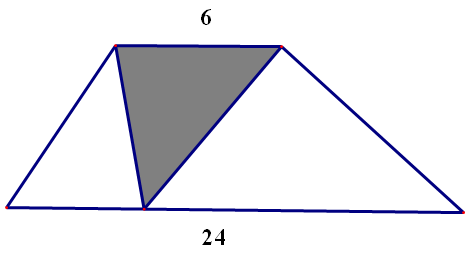
(2月16号)如图,已知梯形的上底是6,下底是24,梯形的面积是60,则阴影部分的面积是_________
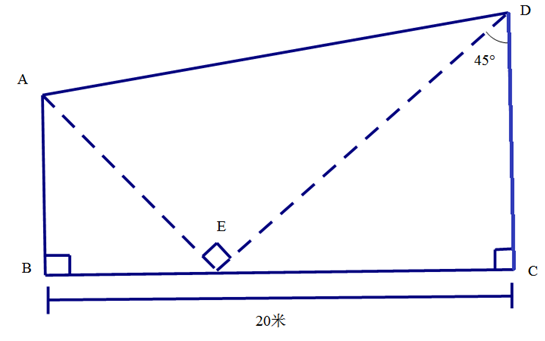
拓展题:某小区有一块如下图所示的梯形空地,根据图中的数据计算,空地的面积是_______平方米。
答案明天公布!!
赶快做一做吧!答对奖励金币哦!
查看昨日答案请点击下页
在公布昨天答案之前,还是先回顾一下旋转和平移法求面积的分别适用范围:
1、旋转法:当已知面积的图形和所求图形没有发生关联,但可以通过旋转使它们发生关联时(特别是当出现了圆的时候,因为四年级还没学到圆的面积计算)
2、平移法:平移法的用法很多,最常见的就是长方形(正方形)中有十字交叉的图纹的时候,可以把条纹全部移到边上。
旋转和平移法也是平面几何里面的经典方法,大家应该很熟练的掌握~
(2月15号答案)如图,最大的正方形的面积是68cm2,则最小的正方形面积是_____cm2
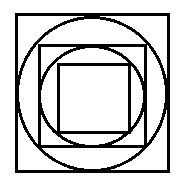
首先,正方形的面积是68,不是完全平方数,要求出边长是不可能的,因此只能够通过找出几个正方形之间的面积关系来求解。
但是我们又发现,这几个正方形之间也没有任何的关联,唯一的联系就是那几个圆。圆我们是没有学过它的面积和周长计算的,能用到的就是它的对称性。这时候,就应该很顺理成章的想到要有旋转法了。
把两个正方形分别旋转到下图的位置,这时候,我们把两个圆忽略掉,是不是就是很经典的图形了。到这里,大家应该都知道该怎么求最小的正方形的面积了,就是68÷2÷2=17cm2
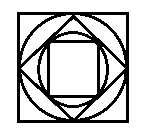
拓展题:下图中空白处的每个方格都是边长相等的正方形,阴影部分的宽度相等。则阴影部分的面积是___________平方厘米。
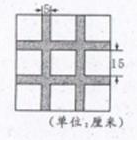
答案:这道题直接算是可以的,但一定要记得把重叠部分(4个小正方形)的面积减去。
更好的方法是通过平移法,把横条和竖条都移到边上去(如下图),这时候,阴影部分的面积就等于整个正方形面积减去空白部分的面积。
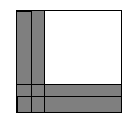
空白部分的面积是(15×3)×(15×3)=2025(平方厘米),整个大正方形面积是(15×3+5×2)×(15×3+5×2)=3025(平方厘米)
所以空白部分的面积是 3025-2025=1000(平方厘米)









