四年级华杯赛备考每日一题(2.12)(2)
在公布昨天答案之前,先回顾一下数字谜的基本做法:
其实最重要的就是四个字,找突破口,只要把突破口找到了,后面的问题就迎刃而解了。
(2月11号)下面的加法算式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,
那么,我+爱+奥+数=___________
我爱奥数
我爱奥
+ 我爱
——————
2 0 0 3
首先,突破口肯定在“我”上面,因为第一位上,“我”加上上一位的进位等于2,而“爱”+“我”的对应位是0,前一位的进位最多是2,“爱”和“我”不可能都是9,所以“爱”+“我”向前一位进位是1。于是,“我”=1;
然后,因为“爱”+“我”+进位的得数是10,“奥”+ 爱”+“我”的对应位是0,十位肯定有进位,所以“爱”+“我”可能是8或者9;
如果 “爱”+“我” 是8,十位向百位就要进2,奥必须是9,8+9=17,个位还要向十位进3,这是不可能的。所以 “爱”+“我” 只能是9,“爱”=8;
“爱”+“我”是9,“奥”+ “爱”+“我”就是10,而个位向十位肯定有进位,所以“奥”只能是0;
剩下个位, “数”+“奥”+“ 爱”=13,所以“数”=5
于是, “我”+ 爱”+“奥”+“数”=1+8+0+5=14
拓展题:如图,在两个圆环内英文字母区域分别填入数字1-9,使得任何两个相邻区域内(有公共边的区域称为相邻区域)的数字的差(大数减小数)至少是2.那么三位数ABC =______
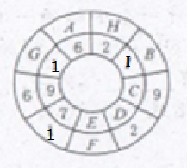
(这道题是希望杯100题里面的第60题,如果图看不清的可以自己看那本希望杯100题,题意是要把内圈和外圈都分别是由1-9来组成。)
答案:这道题的突破口在I,I只能是4,5或者8,但是如果I是4,C就没有可以填的数了。I如果是8,内圈剩下的只有3,4,5,而内圈剩下的格是EDC,连续的三个格填3,4,5,是不可能填进的。于是,I就只能是5了。
填了I之后,C就只能是3了,然后D也就可以确定是8,剩下E填4,内圈填完。
接下来是外圈,外圈的突破口在B,B只能填3或者7。但是,B填7的话,F就只能填8,外圈剩下GAH三个连续的格子,剩下的数只有3,4,5,又是不可能填进的,所以B就只能填3。
B填了3之后,A只能填4或者8。但是如果A填了4,外圈剩下的格子是GHF,剩下的数是5,7,8,发现这三个格子都不能够填5,所以A只能填8.
A填完8之后,G只能填4,于是H只能填5,最后剩下F填7.
所以三位数ABC=833









