小学二年级上册奥数知识点:找规律法(2)
例4 从1开始,每隔两个数写出一个数,得到一列数,求这列数的第100个数是多少?
1,4,7,10,13,…
解:不难看出,这是一个等差数列,它的后一项都比相邻的前一项大3,即公差=3,还可以发现:
第2项等于第1项加1个公差即
4=1+1×3.
第3项等于第1项加2个公差即
7=1+2×3.
第4项等于第1项加3个公差即
10=1+3×3.
第5项等于第1项加4个公差即
13=1+4×3.
…
可见第n项等于第1项加(n-1)个公差,即
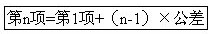
按这个规律,可求出:
第100项=1+(100-1)×3=1+99×3=298.
例5 画图游戏先画第一代,一个△,再画第二代,在△下面画出两条线段,在一条线段的末端又画一个△,在另一条的末端画一个○;画第三代,在第二代的△下面又画出两条线段,一条末端画△,另一条末端画○;而在第二代的○的下面画一条线,线的末端再画一个△;…一直照此画下去(见下图),问第十次的△和○共有多少个?
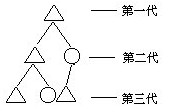
解:按着画图规则继续画出几代,以便于观察,以期从中找出图形的生成规律,见下图.
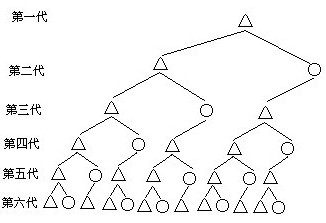
数一数,各代的图形(包括△和○)的个数列成下表:

可以发现各代图形个数组成一个数列,这个数列的生成规律是,从第三项起每一项都是前面两项之和.按此规律接着把数列写下去,可得出第十代的△和○共有89个(见下表):

这就是著名的裴波那契数列.裴波那契是意大利的数学家,他生活在距今大约七百多年以前的时代.
例6 如下图所示,5个大小不等的中心有孔的圆盘,按大的在下、小的在上的次序套在木桩上构成了一座圆盘塔.现在要把这座圆盘塔移到另一个木桩上.规定移动时要遵守一个条件,每搬一次只许拿一个圆盘而且任何时候大圆盘都不能压住小圆盘.假如还有第三个木桩可作临时存放圆盘之用.问把这5个圆盘全部移到另一个木桩上至少需要搬动多少次?(下图所示)
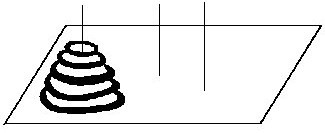
解:先从最简单情形试起.
①当仅有一个圆盘时,显然只需搬动一次(见下页图).
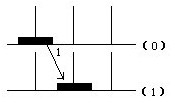
②当有两个圆盘时,只需搬动3次(见下图).
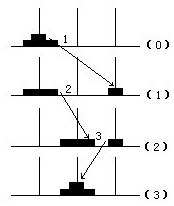
③当有三个圆盘时,需要搬动7次(见下页图).
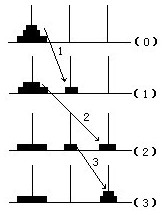
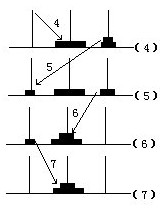
总结,找规律:
①当仅有一个圆盘时,只需搬1次.
②当有两个圆盘,上面的小圆盘先要搬到临时桩上,等大圆盘搬到中间桩后,小圆盘还得再搬回来到大圆盘上.所以小的要搬两次,下面的大盘要搬1次.这样搬到两个圆盘需3次.
③当有三个圆盘时,必须先要把上面的两个小的圆盘搬到临时桩上,见上图中的(1)~(3).由前面可知,这需要搬动3次.然后把最下层的最大圆盘搬一次到中间桩上,见图(4),之后再把上面的两个搬到中间桩上,这又需搬3次,见图中(5)~(7).
所以共搬动2×3+1=7次.
④推论,当有4个圆盘时,就需要先把上面的3个圆盘搬到临时桩上,需要7次,然后把下面的大圆盘搬到中间桩上(1次),之后再把临时桩上的3个圆盘搬到中间桩上,这又需要7次,所以共需搬动2×7+1=15次.
⑤可见当有5个圆盘时,要把它按规定搬到中间桩上去共需要:
2×15+1=31次.
这样也可以写出一个一般的公式(叫递推公式)

对于有更多圆盘的情况可由这个公式算出来.

进一步进行考察,并联想到另一个数列:

若把n个圆盘搬动的次数写成an,把两个表对照后,
可得出

有了这个公式后直接把圆盘数代入计算就行了,不必再像前一个公式那样进行递推了.
| 了解无锡小升初信息渠道: |
| 无锡初中家长群:175986498 无锡小升初家长交流2群:37076654 |
| 无锡奥数网 无锡E度论坛 |

编辑推荐:




