1.先计算下面的前几个算式，找出规律，再继续往下写出一些算式：

　　①1×9+2= ②9×9+7=

　　12×9+3= 98×9+6=

　　123×9+4= 987×9+5=

　　1234×9+5= 9876×9+4=

　　… …

　　2.先计算下面的奇妙算式，找出规律，再继续写出一些算式：

19+9×9=

118+98×9=

1117+987×9=

11116+9876×9=

111115+98765×9=

…

　　3.先计算下面的前几个算式，找出规律，再继续写出一些算式：

1×1=

11×11=

111×111=

1111×1111=

11111×11111=

…

　　4.有一列数是2、9、8、2、…，从第三个数起，每一个数都是它前面的两个数相乘积的个位数字(比如第三个数8就是2×9=18的个位数字).问这一列数的第100个数是几?

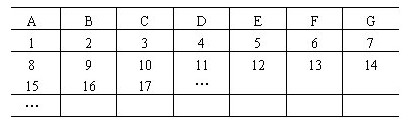
　　5.如果全体自然数按下表进行排列，那么数1000应在哪个字母下面?

　　6.如果自然数如下图所示排成四列，问101在哪个字母下面?

　　7.3×3的末位数字是9，3×3×3的末位数是7，3×3×3×3的末位数字是1.求35个3相乘的结果的末位数字是几?

　　习题解答

　　1解.①1×9+2=11

　　12×9+3=111

　　123×9+4=1111

　　1234×9+5=11111

　　12345×9+6=111111

　　123456×9+7=1111111

　　1234567×9+8=11111111

　　12345678×9+9=111111111.

　　②9×9+7=88

　　98×9+6=888

　　987×9+5=8888

　　9876×9+4=88888

　　98765×9+3=888888

　　987654×9+2=8888888

　　9876543×9+1=88888888.

　　2解.19+9×9=100

　　118+98×9=1000

　　1117+987×9=10000

　　11116+9876×9=100000

　　111115+98765×9=1000000

　　1111114+987654×9=10000000

　　11111113+9876543×9=100000000

　　111111112+98765432×9=1000000000

　　1111111111+987654321×9= 10000000000.

　　3解.

1×1=1

11×11=121

111×111=12321

1111×1111=1234321

11111×11111=123454321

111111×111111=12345654321

1111111×1111111=1234567654321

11111111×11111111=123456787654321

111111111×111111111=12345678987654321

　　4.解：按数列的生成规律再多写出一些数来，再仔细观察，找出规律：

　　2、9、8、2、6、2、2、4、8、2、6、2、2、4、8、2、6、2、2、4、…

　　可见，除最前面的两个数2和9以外，8、2、6、2、2、4这六个数依次重复出现.因此，可利用这个规律，按下面的方法找出第100个数出来：

100-2=98，

98÷6=16…2.

　　即第100个数与这六个数的第2个数相同，即第100个数是2.

　　5.解：不难发现，每个字母下面的数除以7的余数都是相同的.如第1列的三个数1、8和15，除以7时的余数都是1;第2列的三个数2、9和16，除以7时的余数都是2;第3列的三个数3、10和17，除以7的余数都是3;….利用这个规律，可求出第1000个自然数在哪个字母下面：

1000÷7=142…6

　　所以1000在字母F的下面.

　　6.解：可以这样找出排列的规律性：全体自然数依次循环排列在A、B、C、D、D、C、B、A八个字母的下面，即

　　依上题解题方法：

101÷8=12…5.

　　可知101与5均排在同一字母下面，即在D的下面.

　　7.解：从简单情况做起，列表找规律：

　　仔细观察可发现，乘积的末位数字的出现有周期性的规律：看相乘的3的个数除以4的余数，

　　余1时，积的末位数字是3，

　　余2时，积的末位数字是9，

　　余3时，积的末位数字是7，

　　整除时，积的末位数字是1，

　　35÷4=8…3

　　所以这个积的末位数字是7.