1.两数的乘积是整十、整百、整千的，要先乘。为此要牢记下面这三个特殊的等式：

　　5×2=10

　　25×4=100

　　125×8=1000

　　例1计算①123×4×25

　　②125×2×8×25×5×4

　　解①123×4×5=123×(4×25)=123×100=12300

　　②125×2×8×25×5×4=(125×8)×(25×4)×(5×2)=1000×100×10=1000000

　　2.分解因数，凑整先乘

　　例计算①24×25

　　②56×125

　　③125×5×32×5

　　解：①24×25=6×（4×25）=600

　　②56×125=7×（8×125）=7000

　　③125×5×32×5=（8×125)×(4×25)=100000

　　3.应用乘法分配律

　　例3.计算

　　①175×34+175×66

　　②67×12+67×35+67×52+6

　　解①175×34+175×66=175×（34+66）=175×100=17500

　　②67×12+67×35+67×52+6=67×（12+35+52+1）=67×100=6700

　　（原式中最好一项67可看成67×1）

　　例4.计算①123×101

　　②123×99

　　解①123×101=123×(100+1)=12300+123=12423

　　②123×99=123×(100-1)=12300-123=12177

　　4.几种特殊因数的巧算

　　例5一个数×10，数后添0；

　　一个数×100，数后天00；

　　一个数×1000，数后天000；

　　以此类推

　　如：15×10=150

　　15×100=1500

　　15×1000=15000

　　例6.一个数×9，数后添0，再减此数；

　　一个数×99，数后添00，再减此数；

　　一个数×999，数后添000，再减此数；

　　以此类推

　　如：12×9=120-12=108

　　12×99=1200-12=1188

　　12×999=12000－12=11988

　　例7.一个偶数乘以5，可以除以2添上0

　　如：6×5=30

　　16×5=80

　　116×5=580
   

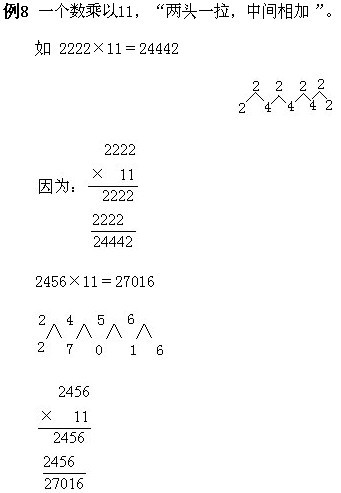
　　例9.一个偶数乘以15，“加半添0”

　　24×15=（24+12）×10=360

　　因为

　　24×15

　　=24×（10+5）

　　=24×（10+10÷2）

　　=24×10+24×10÷2（乘法分配律）

　　=24×10+24÷2×10（带符号搬家）

　　=（24+24÷2）×10（乘法分配律）

　　例10个位为5的两位数的自乘：十位数字×（十位数字加1）×100＋25

　　如15×15=1×(1+1)×100+25=225

　　25×25=2×(2+1)×100+5=625

　　35×35=3×(3+1)×100+25=1225

　　45×45=4×（4+1）×100+25=2025

　　55×55=5×（5+1）×100+25=3025

　　65×65=6×（6+1）×100+25=4225

　　75×75=7×（7+1）×100+25=5625

　　85×85=8×（8+1）×100+25=7225

　　95×95=9×(9+1)×100+25=9025

　　还有一些其他特殊因数相乘的简便算法，有兴趣的同学可参看《算的快》一书