数数与计数(一)
数学需要观察.大数学家欧拉就特别强调观察对于数学发现的重要作用,认为“观察是一件极为重要的事”.本讲数数与计数的学习有助于培养同学们的观察能力.在这里请大家记住,观察不只是用眼睛看,还要用脑子想,要充分发挥想像力.
例1 数一数,图2-1和图2-2中各有多少黑方块和白方块?
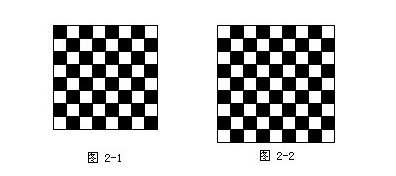
解:仔细观察图2-1,可发现黑方块和白方块同样多.因为每一行中有4个黑方块和4个白方块,共有8行,所以:
黑方块是:4×8=32(个)
白方块是:4×8=32(个)
再仔细观察图2-2,从上往下看:
第一行白方块5个,黑方块4个;
第二行白方块4个,黑方块5个;
第三、五、七行同第一行,
第四、六、八行同第二行;
但最后的第九行是白方块5个,黑方块4个.可见白方块总数比黑方块总数多1个.
白方块总数:5+4+5+4+5+4+5+4+5=41(个)
黑方块总数:4+5+4+5+4+5+4+5+4=40(个)
再一种方法是:
每一行的白方块和黑方块共9个.
共有9行,所以,白、黑方块的总数是:
9×9=81(个).
由于白方块比黑方块多1个,所以白方块是41个,黑方块是40个.
例2 图2-3所示砖墙是由正六边形的特型砖砌成,中间有个“雪花”状的墙洞,问需要几块正六边形的砖(图2-4)才能把它补好?
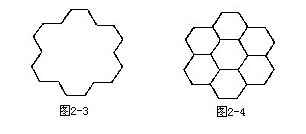
解:仔细观察,并发挥想象力可得出答案,用七块正六边形的砖可把这个墙洞补好.如果动手画一画,就会看得更清楚了.
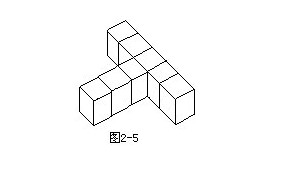
例3将8个小立方块组成如图2-5所示的“丁”字型,再将表面都涂成红色,然后就把小立方块分开,问:
(1)3面被涂成红色的小立方块有多少个?
(2)4面被涂成红色的小立方块有多少个?
(3)5面被涂成红色的小立方块有多少个?
解:如图2-6所示,看着图,想像涂色情况.当把整个表面都涂成红色后,只有那些“粘在一起”的面(又叫互相接触的面),没有被涂色.每个小立方体都有6个面,减去没涂色的面数,就得涂色的面数.每个小立方体涂色面数都写在了它的上面,参看图2-6所示.
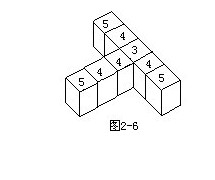
(1)3面涂色的小立方体共有1个;
(2)4面涂色的小立方体共有4个;
(3)5面涂色的小立方体共有3个.
例4如图2-7所示,一个大长方体的表面上都涂上红色,然后切成18个小立方体(切线如图中虚线所示).在这些切成的小立方体中,问:]

(1)1面涂成红色的有几个?
(2)2面涂成红色的有几个?
(3)3面涂成红色的有几个?
解:仔细观察图形,并发挥想像力,可知:
(1)上下两层中间的2块只有一面涂色;
(2)每层四边中间的1块有两面涂色,上下两层共8块;
(3)每层四角的4块有三面涂色,上下两层共有8块.最后检验一下小立体总块数:
2+8+8=18(个).




