六年级奥数应用题及答案:几何路程题(2)
奥数网整理
2011-07-25 15:45:21
答案:
我们首先想到将桶的圆柱面展开成矩形平面图(下图),由于B点在里面,不便于作图,设想将BD延长到F,使DF=BD,即以直线CD为对称轴,作出点B的对称点F,用F代替B,即可找出最短路线了。
解:将圆柱面展成平面图形(上图),延长BD到F,使DF=BD,即作点B关于直线CD的对称点F,连结AF,交桶口沿线CD于O。
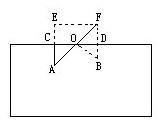
因为桶口沿线CD是B、F的对称轴,所以OB=OF,而A、F之间的最短线路是直线段AF,又AF=AO+OF,那么A、B之间的最短距离就是AO+OB,故蚂蚁应该在桶外爬到O点后,转向桶内B点爬去。
延长AC到E,使CE=DF,易知△AEF是直角三角形,AF是斜边,EF=CD,根据勾股定理,AF2=(AC+CE)2+EF2
=(12+8)2+152=625=252,解得AF=25。
即蚂蚁爬行的最短路程是25厘米。
相关阅读:





