每次当你拿起电话听筒打电话，发传真，或发调制解调器信息时，你就进入了非常复杂的巨大网络。覆盖全球的通信网是惊人的。很难想像每天有多少次电话在这网络上打来打去。一个系统被不同国家和水域的不同系统“分割”，它是如何运行的呢？一次电话是如何通向在你的城市、你的国家或另一国家中的某个人的呢？

在早期电话史上，打电话的人拿起电话听筒，摇动曲柄，与接线员联系。一位本地接线员的声音从本地交换台来到线上，说“请报号码”，然后他把你同你试图通话的对方连接起来。如今，这一过程由于有了各种不同的转换和送达通话的方法而如雨后春笋般地迅速发展。包含着线性规划的各种复杂类型，以及有关的二进制和二进编码的数学，已脱离了潜在的不稳固地位而成为有意义的东西。

你的声音是如何行进的？你的声音产生声波，在听筒中转换成电信号。今天，这些电脉冲可以用许多不同的方法传递和转换。它们可以变成激光信号，然后沿光纤电缆传递①；它们可以转换成无线电信号，然后利用无线电或微波线路在一个国家内从一座塔传送到另一座塔；或者它们可以仍旧作为电信号沿着电话线传送。在美国，大部分电话都是由自动交换系统接通的。现在电子交换系统是最快的。这系统有一个程序，这程序包含电话运行的所有方面所需的信息，并且时刻在了解哪些电话正在使用，哪些通道是可用的。通话可以由不同频率的电流传送，或转换成数字信号。这两种方法都使多重通话可以沿同一些电线传送。最新式的系统把通话转换成数字信号，然后再用二进制数列编码。于是各个通话可以沿着线路以特定的次序“同时”行进，直到它们被译码而到达各自的目的地。

1947年，数学家乔治B．丹齐克研究出了求解复杂线性规划问题的单纯形法。单纯形法实质上是沿着那立体的棱进行，依次检查每一隅角，并总是向着最优解前进。当可能解的数目不超过15000～20000时，这方法能有效地求得解答。1984年，数学家纳伦德拉·卡马卡发现一种方法，它使求解很麻烦的线性规划问题例如长距离电话最优通话线路问题所需的时间大为缩短。卡马卡算法采取了一条通过那立体内部的捷径。在选择了一个任意内点之后，这算法使整个结构变形，以把问题改造得使所选择的点正好在那立体的中心。下一步是朝着最优解的方向找到一个新的点，再将结构变形，又使新点位于中心。必须进行变形，否则那些看来能给出最优改进的方向都是虚假的。这些重复的变换以射影几何的概念为基础，很快便能得到最优解。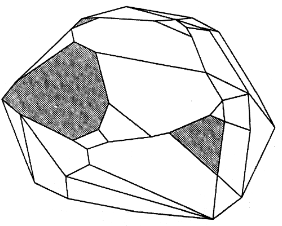

打电话时，电话系统选择最佳通话途径，并发出一连串指令，以接通线路。整个过程只需几分之一秒。通话线路最好是直接通向对方的——从节省距离和时间的观点看来，这是人们所期望的。但是如果直接线路正在为别的通话服务，新的通话就必须沿其他线路中最好的一条进行。这正是需要用到线性规划②的地方。我们把电话线路问题当作一个有几百万个面的复杂几何立体形来看。每个顶点代表一个可能的解。问题是要找出最优解，而不必计算每一个解。

今天，古老的电话敬语“请报号码”具有双重的意义。曾经是简单的拿起电话听筒打电话的过程，现在却要使一个依靠着数学的庞大而复杂的网络运作起来。

①“同时”通话数可从96到13000以上，这视所用线路类型而定。光纤系统能比传统的铜/铝缆运载更多的信息。

②线性规划技术可用来解决许多不同的问题。这些问题通常有许多条件和变量。可以用一个农业问题作简单例子：一个农民要想决定如何最有效地利用他（她）的土地使产量和收益达到最大。条件和变量包括诸如这些事情：考虑不同的作物，每种作物需要多少土地，每种作物单产多少，每种作物售出后获得多少收入。为解这样一个问题，人们就每一条件写出线性不等式和/或方程，并在二维坐标图中一个多边形区域上求解。