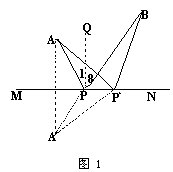
解：作A关于MN的对称点A′，连A′B交MN于点P，则光线将由A射到P，经反射后到B，这条路线是“最短路线”。实际上，对MN上任一非P的点P，都有AP′+P′B=AP′+P′B＞A′B=AP+PB。即这条路线最短。

　　由此可得到物理学中的反射定律：光经平面镜反射时，入射角等于反射角，在图1中，取P点处法线PQ，则有∠1=∠2。

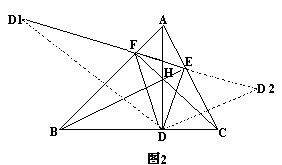
　　在△ABC中，AD、BE、CF分别为三边上的高，△DEF称为△ABC的垂足三角形，可以证明△ABC的重心H是△DEF的内心（图2）。

　　实际上，由∠BEA=∠BDA=90°，知B、D、E、A共圆，于是∠CDE=∠BAC。同样，由A、F、D、C共圆，可知∠BDF=∠BAC，于是∠CDE=∠BDF。从而可知DA平分∠EDF。

　　同理FC平分∠DFE，EB平分∠DEF。故H是△DEF的内心。

　　如作D关于AB的对称点D1，可知∠DFB=∠D1FB＝∠AFE，于是，D1、F、E在一直线上。同样可知，D关于AC的对称点D2也在直线EF上，即D1、F、E、D2四点在一条直线上。

　　现在，我们来看由法格拉洛提出的一个问题：在△ABC的每条边上各取一点D、E、F，△DEF称为△ABC的内接三角形。试在锐角三角形ABC的所有内接三角形中，求周长最短的三角形。

　　费尔马提出了一种解法，这个解法分成三步来解：

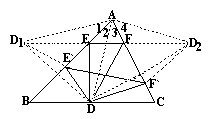
　　（1）设D是BC上固定点，求此时的周长最短的内接三角形。

　　作D关于AB、AC的对称点D1、D2，连D1D2交AB、AC于E、F，则△DEF为所求。实际上，对于△ABC的任一内接△DE′F′，有

　　DE′+E′F′+F′D=D1E′+E′F′+F′D2

　　≥D1D2=D1E+EF+FD2

　　=DE＋EF＋FD。

　　就是△DEF的周长≤△DEF的周长。

　　因此，我们只要对于每一个BC上的点D，都找出相应于该点的周长最短的内接三角形DEF，在这些三角形中找出周长最短的一个就行。

　　（2）由于 AD1=AD，AD2=AD，故△AD1D2是等腰三角形。又由于∠1=∠2，∠3=∠4，故△AD1D2的顶角∠D1AD2=2∠BAC为定值，因此，只有当其腰AD1最短时，D1D2最短。此时必有AD最短。从而当 AD为△ABC的高时，内接三角形DEF的周长最短。

　　（3）当AD为△ABC的高时，由前面三角形垂足三角形性质，可证△ABC的内接三角形中，以其垂足三角形DEF的周长最短。

　　在平面几何中，还有一个以费尔马为名的“费尔马点”。即：在△ABC所在平面上找一点，它到三个顶点的距离之和相等。

　　只考虑△ABC的三个内角都小于120°的情况。

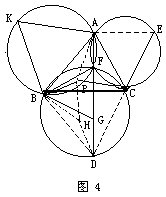
　　以 AB、BC、CA为边向形外作正三角形BCD、ACE、ABK，作此三个三角形的外接圆。设⊙ABK、⊙ACE除A外的交点为F，由 A、K、B、F四点共圆知∠AFB＝120°。同理∠AFC＝120°于是∠BFC=120°。故⊙BCD边过点F，即⊙ABK，⊙BCD，⊙CAE共点F。

　　由∠AFB=120°，∠BFD=60°，知 A、F、D在一条直线上。

　　在FD上取点G，使FG=FB，则△FBG为正三角形。由BG＝ BF， BD＝BC，∠DBG＝∠CBF＝60°-∠GBC，故△DBG≌△CBF。于是GD＝FC，即AD=FA+FB+FC。

　　对于平面上任一点P，以BP为一边作等边△PBH（如图4），连HD，同样可证△BHD≌△BPC。于是AP+PH+HD=PA+PB+PC。但PA+PH+HD≥AD=FA+ FB+FC。这就是说，点F为所求点。这点称为△ABC的费尔马点。

　　如果△ABC有某一内角≥120°，例如∠A≥120°，则点A即为所求点。