第十届“希望杯”全国数学邀请赛复赛六年级试题
下面是重庆奥数网整理的2012年重庆小学希望杯复赛六年级试题,供大家参考学习。
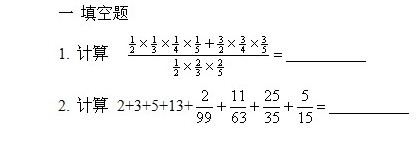
3.王涛将连续的自然数1,2,3……逐个相加,一直到某个自然数为止,由于计算时漏加了一个自然数而得到错误的结果,那么,他漏加的自然数是______ 。
4.在数0.20120415中的小数点后面的数字上方加上循环小树,而这些循环小数中最大的是 ,最小的是 ______ 。

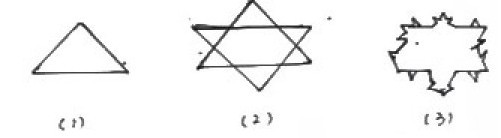
6. 对于一个多边形,定义一种“生长”操作:如图1,将其一边AB变成向外凸的折线ACDEB,其中C和E是AB 的三等分点,C、D、E三点可构成等边三角形,那么,一个边长是9的等边三角形,经过两次“生长”操作(如图2),得到的图形的周长是 ,经过几回“生长”,得到的图形的周长是______ 。
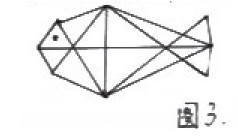
7. 如图3所示的“鱼形图案中共有______ 三角形。
8. 已知自然数N的个位数字是0,且有8个约数,则N最小是______ 。
9. 李华在买某种商品的时候,将单价中的某一数字“1”错看成了“7”,准备付款189元,实际付147元。已知商品的单价及购买的数量都是整数,则这种商品的实际单价是 元,李华共买了 ______ 件。
10. 如图4,已知AB=40cm,图中的曲线是由半径不同的半圆弧平滑连接而成,那么阴影部分的面积是______ cm2 (π取3.14)


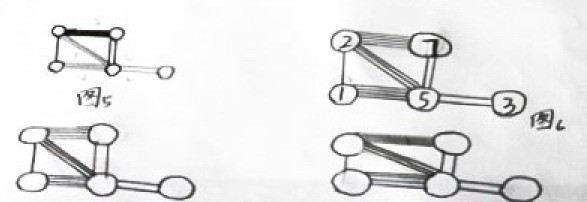
13. 将1到9这9个自然数中的5个数填入图5所示的圆圈内,使任意有线段相连的两个圆圈内的两数之差恰好等于连接着两个圆圈的线段的条数,图6给出了一种填法,请你再给出两种不同的填法。
14. 甲、乙两人分别从A、B两地同时出发相向而行,于C地相遇后,甲继续向B地行走,乙则休息14分钟后再继续向A地行走,甲和乙各自到达B地和A地后,立即折返,又在C地相遇,已知甲每分钟走60米,乙每分钟走80米,则A、B两地相距多少米?
15. 将100个棱长为1的立方体堆放成一个长方体,将可能堆成的多面体的表面积按从小到大排列,求开始的6个。
16.在m行n列的网格中规定:由上而下的横行依次为第1行,第2行……,由左 向右的竖列依次为第1列,第2列,……,点(a,b)表示位于第a 行,第b列的格点,图7是4行5列的网格,从点A(2,3)出发,按象棋中的马走“日”字格的走法,可到达网格中格点 B(1,1),C(3,1),D(4,2),E(4,4),F(3,5),G(1,5),如果在9行9列的网格中(图8),从点(1,1)出发,按象棋中 的马走“日”字格的走法,
(1)能否到达网格中的每一个格点
答: (填“能”或“不能)
如果能,那么沿最短的路线到达某个格点,最多的需要几步?这样的格点有几个?写出它们的位置,如果不能,请说明理由。
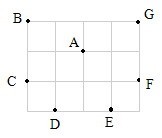
图7

图8
第十届小学希望杯决赛试题详解》》点击查看
第十届“希望杯”全国数学邀请赛复赛六年级试题》》点击下载








