北京五年级数学花园探秘辅导:计数问题
北京奥数网:小编为大家整理了北京五年级数学花园探秘的计数问题辅导练习题,题目解析清楚详细,对数学花园探秘备考很有帮助。
计数问题:
1.计数问题之排列组合:区分好排列和组合的应用条件,组合常用的巧算公式必须要掌握好。掌握排列组合的几种解题方式:插板法、捆绑法、排除法等。
题目:某年级6个班的数学课,分配给甲、乙、丙三名数学老师任教,每人教两个班,分派的方法有多少种?

2.加乘原理:在做一件事时,有几类不同的方法,分类用加法;在做一件事时,要分几步才能完成,分步用乘法。
题目:玩具厂生产一种玩具棒,共4节,用红、黄、蓝三种颜色给每节涂色。这家玩具厂共可生产_______种颜色不同的玩具棒?
方法一:分三类:
(1)只有一种颜色的有3种;
(2)有两种颜色:第一步先从3中颜色中选取两种,有C23=3种,第二步,对于确定的两种颜色,如红色和蓝色的排法进行枚举:
1个红色:蓝蓝蓝红,蓝红蓝蓝
2个红色:红红蓝蓝,红蓝蓝红,红蓝红蓝,蓝红红蓝
3个红色:红红红蓝,红蓝红红
共8种,所以共:3×8=24种。
(3)有三种颜色:第一步选择一种颜色染两节,有3种选法;第二步,假设用红色染两节,这时染色方法为C24×A22÷2=6种。3×6=18种。
所以共有:3+24+18=45种。
方法二:总体—重复
每节有3种涂法,共有涂法3×3×3×3=81(种)。但上述81种涂法中,有些涂法属于重复计算,这是因为有些游戏棒倒过来放时的颜色与顺着放时的颜色一样,却被我们当做两种颜色计算了两次。可以发现只有游戏棒的颜色关于中点对称时才没有被重复计算,关于中点对称的游戏棒有3×3×1×1=9(种)。故玩具棒最多有(81-9)÷2+9=45种不同的颜色。
3.掌握两量重叠和三量重叠的计算公式,韦恩图可以帮助解决大问题。

【解析】
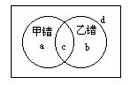
(法一)设共有n道题.由上图知d即为所求,并有关系式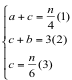
由(1)(3)知,n是4和6的公倍数,即12的倍数。将(3)代入(2),有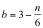
由于b是非负整数,所以n=12,由此求出c=2,b=1,a=1.又由a+b+c+d=n,得到d=n-(a+b+c)=8
(法二)显然两人都答错的题目不多于3道,所以题目总数只可能是6、12、18,其中只有12,能使甲答错题目总数是整数.
【答案】8道题
4.几何计数:常用的方法有枚举法、加法原理和乘法原理法以及递推法等。
分类:数线段、角、三角形、长方形。
掌握n条直线、n个圆(n个三角形、n个四边形)可将平面最多分成多少部分。
题目:该图中有_____个三角形?
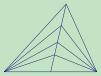
【关键词】2007年,第12届,华杯赛,五年级,决赛,第6题
【解析】由1个,2个,3个,4个,6个,8个小三角形组成的三角形分别有:8,7,4,3,1,1个,也即一共有8+7+4+3+1+1=24个。
【答案】24
编辑推荐:
2016北京数学花园探秘备考:历年真题
北京五年级数学花园探秘辅导:数论问题
北京五年级数学花园探秘辅导:计算问题









